“除数是整数的小数除法”教学实录

教学内容
人教版《数学》五年级上册第三单元“小数除法”例1、例2。
教学目标
1.在有余数除法的基础上自主探索整数除以整数商是小数的小数除法,借助计数器理解除的过程中计数单位的变化。
2.借助整数除法的经验,自主探索小数除以整数的笔算过程,在对比沟通中掌握算法。
3.借助计数器,理解“添0继续除”“商的小数点与被除数小数点对齐”“计算过程不加小数点”的算理。
4.体会小数除法与现实生活的联系,学会思考数学问题的方法,培养提出问题、分析问题和解决问题的能力,发展运算能力。
教学过程
一、温故引新,设疑激趣
1.复习整数除法
师:同学们,今天夏老师带来了2道二年级同学的除法算式,请你们快速写出它们的笔算过程。
出示: 24÷4= 21÷5=
学生独立完成。
师:(出示答案)写对的请举手。

2.引发思考,自主探索
师:恭喜你们已经成功达到二年级小朋友的水平。
生(哄堂大笑):老师,我们都五年级啦!
师:是啊,五年级就该拿出五年级学生该有的水平。二年级时我们知识有限,除到余数1就结束了,但是现在你们真的觉得余数1不能再继续除以5了吗?
生:可以。
师:好,那就请你在原来竖式的基础上继续除下去。
【设计意图】为激发学生的探究欲望,沟通新旧知识之间的联系,根据学生实际,调整了教材中例题的顺序,先教学例2“整数除以整数,商是小数”的情况。这样的安排充分调动了学生对除法意义以及小数意义的已有认知经验,引导学生从有余数的整数除法过渡到小数除法,有利于算理的理解和算法的迁移,也 有利于学生更深刻地理解小数的意义。
二、探究“整数除以整数”
1.理解计数单位的变化
师:这里有两位同学的解答,答案都是4.2,你同意吗?
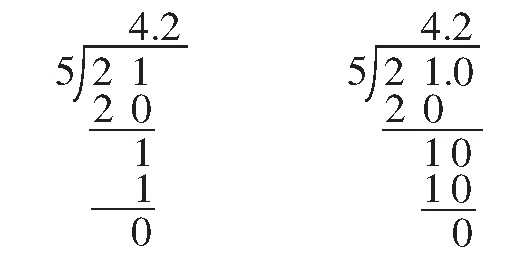
(多数学生表示赞同)
师:仔细观察这两个竖式的笔算过程,有什么不同点?
生:一个下面是1,一个下面是10。
师:你觉得哪一种书写方式更有道理?(学生陷入思考)
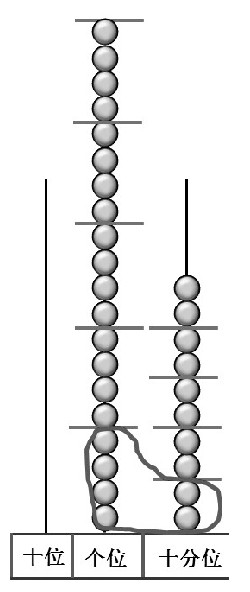
师:21÷5是把21平均分成5份,(出示下图)你能结合计数器说一说21是如何平均分成5份的吗?
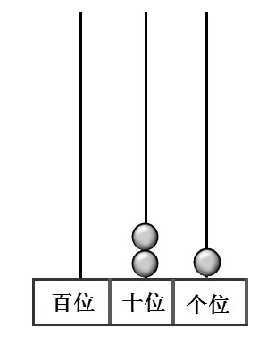
师:十位上的2颗珠子够不够平均分成5份?
生:不够。
师:怎么办?
生:把十位上的2颗珠子移到个位。
生:把2个十转化为20个一。
师:要想数量变多,就要单位变小。把2个十换成20个一,一共就有21个一。这样够分了吗?怎么分?
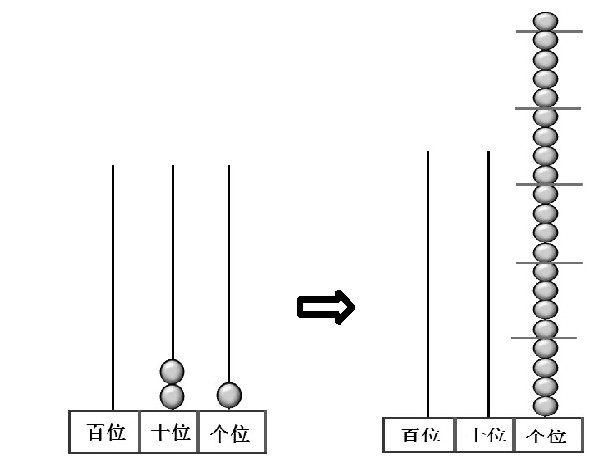
生:21个一平均分成5份,每份分得4个一,还余1个一。
师:那余下的1个一还能不能继续在个位上平均分成5份?
生:不能。
师:怎么解决?
生:将个位上的1颗珠子移到十分位上,变成10颗珠子。
师:要想数量变多,就要单位变小。把1 个一转化成10个十分之一,再将10个十分之一平均分。所以,你觉得哪一种竖式写法更能体现把10个十分之一平均分的过程?
生:第二种,这个10表示10个十分之一。
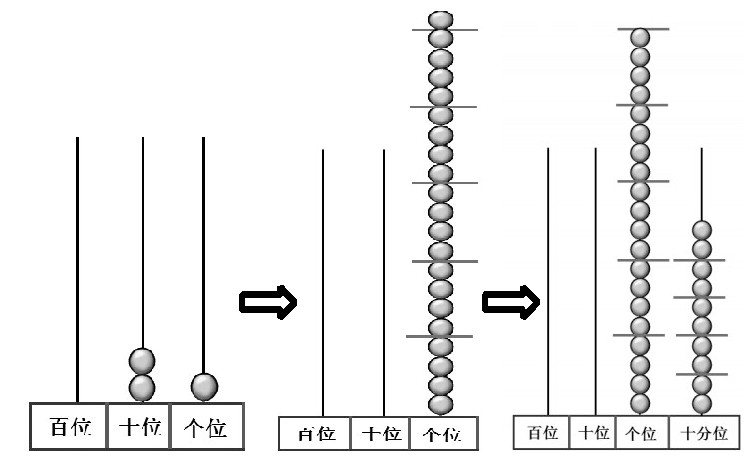
2.理解“被除数的末尾添0”
师:被除数的后面没有数了,“10”的这个0 是哪里来的?
生:在被除数右下角点上小数点,后面添上0。
师:对了,被除数的右下角其实有一个隐形的小数点。为什么可以在被除数的末尾添上0?
生:在小数的末尾添上0或者去掉0,小数的大小不变。
师:这是我们学过的小数的基本性质。
3.理解小数点的位置
师:这个“10”表示什么意思?
生:10个十分之一。
师:然后怎么分?
生:10个十分之一平均分成5 份,每份分得2个十分之一。
师:所以,2要写在什么位上?
生:十分位。
师:怎么体现2在十分位上?
生:在2的前面加上小数点。
师:所以,每份分得的结果是 4个一和2个十分之一,是4.2。(上图)
4.对比提升
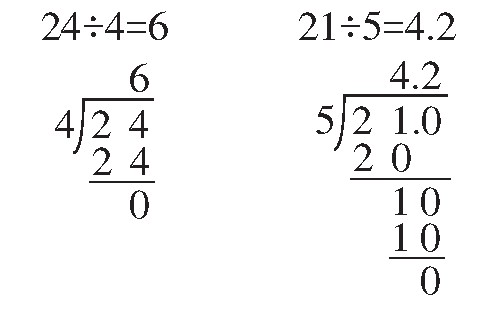
师:二年级时,我们学习了有余数的除法,知道整数除法有些恰好分完,没有余数;有些分不完,有余数。经过三年级认识小数,四年级学习小数的意义,我们知道可以把余数的计数单位变小,让它的数量变多,然后继续除下去,这就是我们今天学习的小数除法。只是这时候整数除以整数,商变成了小数。
师:你觉得还有什么除法,结果可能也是小数?
生:小数除以小数。
生:小数除以整数。 ……
【设计意图】除法是一个平均分的过程,每次分都是把“余数”的计数单位变小和低一位上的数合并继续分的过程。如何将抽象的算理直观化?借助计数器这一直观模型,引导学生将“分 —换—再分”这一平均分的过程,与竖式运算中的“除—添‘0’—再除”的过程建立联系,使学生直观理解“添0”的过程就是当大计数单位不够分时转化为数量更多的小计数单位的过程。本环节借助计数器较好地凸显了除法中的“添0”就是“计数单位转换”这一核心。
三、自主探索 “小数除以整数”
1.迁移类比,自主探索
师:接下来,我们就来研究小数除以整数。22.4÷4,你会做吗?
学生尝试笔算,教师巡视并挑选了两幅作品。
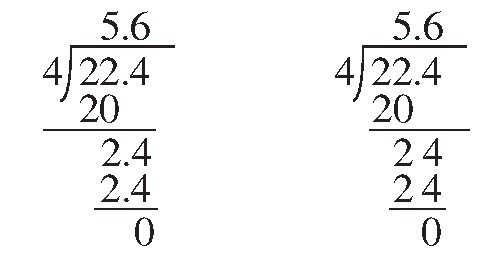
2.借助直观,理解算理
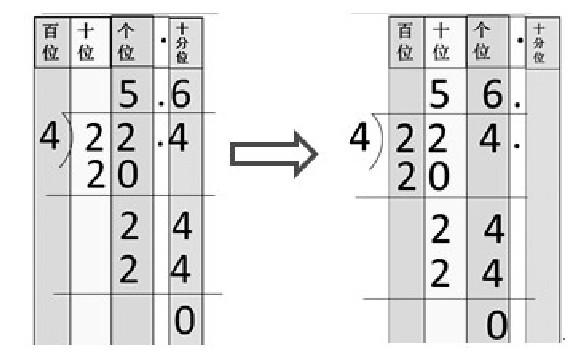
师:仔细观察,这两个竖式有什么不同?
生:一个下面是2.4,一个下面是24。
师:写2.4和写24表示的大小一样吗?为什么?
生:不一样。
生:我认为是一样的,因为2在个位,4在十分位,都表示24个十分之一,大小相同。
师:其实,竖式后面有一张隐藏的数位顺序表。
(课件出示下图)你看到了吗?
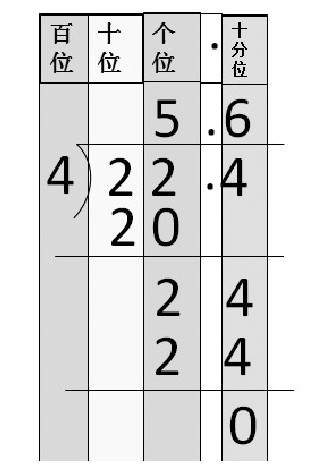
师:基于图示,你认为写哪个更符合平均分的过程呢?
生1:因为被除数22.4有小数点,我认为这个小数点也应该落下来,所以写2.4。
生2:因为我们算的时候其实是在算24÷4=6,所以写24比较好算。
生1:那你这样就变成24了,应该是2.4。
生2:虽然写24,但表示的是24个十分之一,和写2.4是一样的,写24更好算。
(生1点头表示同意)
生3:既然一样,写2.4更清楚啊,因为被除数有小数点。
生2:因为我们是用24个十分之一去平均分的。2.4平均分成4份不好分,所以写24。
生3:我也无话可说了。
师:判断这里写2.4还是24,其实就是思考剩下的2个一和4个十分之一怎样继续平均分成4份。请你想象一下,个位上的2颗珠子和十分位上的4颗珠子,我们是怎样继续平均分成4份的?
生:个位上的2颗珠子不够分,可以转化到十分位上,变成20颗珠子。
师:要想数量变多,就要把单位变小。把2个一看成20个十分之一,再加上原来的4个十分之一,一共就有24个十分之一。所以,写什么更符合平均分的过程?
生:写24,表示24个十分之一。
师:那每份分得多少?怎么表示?
生:每份分得6个十分之一,在6的前面加上小数点。
3.新旧对比,沟通算法
师:小数除以整数我们之前没有学过,你们怎么会笔算?
生:根据整数除法的方法去算。
师:怎么想到按照整数除法的方法去算呢?
生:我们在第一单元学习小数乘法时就是把小数乘法转化为整数乘法来计算的,所以觉得小数除法应该也可以这样做。
师:把小数乘法的经验迁移到小数除法中,很会思考和学习。那么,你觉得小数除法和整数除法最大的不同是什么?
生:多了小数点。
师:多了一个小数点,相当于每个数所在的数位发生了变化。
(课件演示移动数位表)
师:你发现了什么?
生:在22.4÷4的基础上把小数点向右移动一位,就变成224÷4。
师:把22.4的小数点向右移动一位,就是把被除数扩大到原来的10倍,除数不变,商也会扩大到原来的10倍,这让你想到了以前学过的什么?
生:商的变化规律。
师:所以,就可以把22.4÷4看成224÷4来计算。要使商不变,还要怎么做?
生:把56缩小到原来的十分之一,小数点要向左移动一位。
师:想象一下,继续向左移动一位,算式是什么?
生:2.24÷4=0.56。
师:仔细观察这三个竖式,它们有什么相同点?

生:下面都是24。
生:竖式下面部分都是一样的。
师:这三个竖式中的20和24表示的意思一样吗?
生:不一样,三个竖式中的20分别表示20个十、20个一、20个十分之一。
生:三个竖式中的24分别表示24个一,24个十分之一,24个百分之一。
师:其实,分的过程和方法是一样的,只是每次分的计数单位不同。
师:你觉得还有哪些除法算式也可以看成224÷4来计算?
生:0.224÷4,2240÷4……
师:所以,小数除以整数,我们可以怎么笔算?
生:按照整数除法的方法,最后加上小数点。
师:在小数除法中,如何快速判断相同数位是否对齐?
生:只要商的小数点和被除数的小数点对齐就可以了。
【设计意图】因为有了整数除以整数算法 理解的基础,本环节的小数除以整数,给足思考的时间和探究的空间,放手让学生独立思考、自主尝试、辩论交流。在师生和生生交流中,学生借助计数器理解算理,并基于整数除法的经验初步感知算法。为了进一步打通整数除法与小数除法之间的联系,教师借助数位顺序表的移动,沟通商的变化规律,引导学生自主归纳算法。
四、练习巩固,学以致用
师:三位同学去三家商店买同样的笔记本,这是他们的购买情况——小明去甲商店买6本共花37.5元;小玲去乙商店买7本共花42.56元;小军去丙商店买4 本共花29元。哪家店最实惠?
师:你能先快速排除一家商店吗?
生:丙商店。通过估算可以知道,甲商店和乙商店的单价都小于7,但是丙商店的单价一定大于7。
师:估算是解决问题的好方法,到底是甲还是乙最实惠呢,这就需要准确计算。请同学们动笔算一算。
学生笔算37.5÷6和42.56÷7。
集体交流时展示错例,学生做小老师改错,着重说明37.5÷6十分位上要继续添0以及42.56÷7中十分位上不够商1要商0。
师:丙商店的老板发现生意越来越差,非常苦恼,他想知道自己的标价比甲店、乙店贵多少元,你能帮帮他吗?
学生笔算29÷4。
师:在计算29÷4的时候,你发现了什么?
生:添1次0还不够,要添2次0。
教师引导学生结合计数器解释每一步计算的过程(如下)。
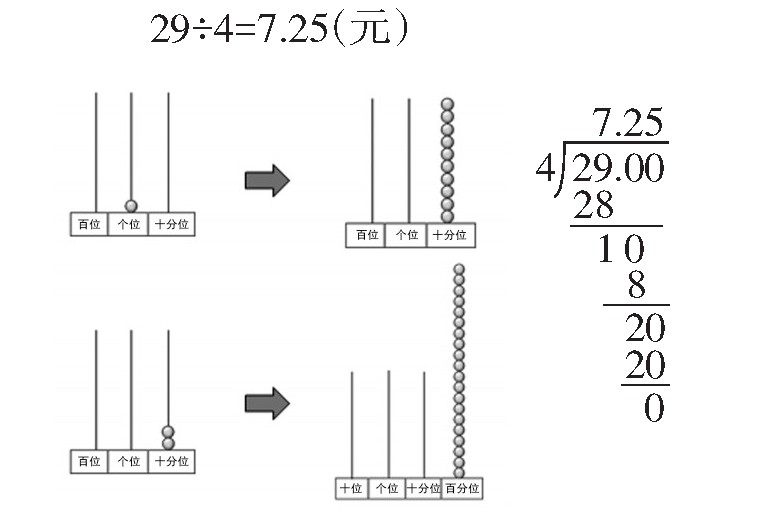
生:先用29除以4,商7还余1;1除以4不够除,所以在1的末尾添上0,看成10个十分之一继续除,商2余2;2个十分之一除以4不够除,所以再在2的末尾添上0,看成20个百分之一;20个百分之一除以4,每份是5个百分之一,所以结果是7加2个十分之一加5个百分之一,等于7.25。
师:每次除,都是在余数末尾添上0,把大的计数单位变成小的计数单位。
【设计意图】练习是巩固知识、形成技能、发展智力的重要环节。本着“算用结合”“一题多用”的原则,教师设计了一道综合性问题,一方面将估算和笔算结合,凸显估算的应用价值;另一方面在笔算的难度上又是一次提升,放手让学生自主探索商中间有0和余数末尾连续添0的笔算,促进知识的迁移和应用。
五、全课小结,拓展延伸
师:想象一下,如果还有余数呢?
生:继续添0。
师:还有余数呢?
生:再添0。
师:是不是只要一直添0,就一定能除尽?
生:不一定,比如10÷3,20÷6……
师:我们一起来算一算10÷3。
生:10÷3,商3余1;1除以3不够除,在1的末尾添上0,看成10个十分之一继续除,商3余1;1除以3不够除,在1的末尾添上0,看成10 个百分之一继续除……
师:你发现了什么?
生:一直余1,永远除不尽!
生:答案是3.33333……
师:不妨一起回顾一下我们学习的历程。同学们先认识了整数,学习了加减乘除,加、减、乘都可以得到整数的结果,但是算除法时,我们发现有些可以恰好分完,没有余数,有些分不完,有余数。但数学在发展,你们也在进步,小数的出现帮助我们解决了有余数除法的难题,我们发现只要将余数的计数单位变小, 让它的数量变多,就可以继续除下去。但是人们又发现,有些除法不管怎么添0,一直都除不尽,那该怎么办呢?学习就是这样不停地发现问题、解决问题、再发现问题的过程!
【设计意图】课的最后进行适当延伸,在具体的例子中让学生体会到不是所有的除法通过在余数末尾添0都可以除尽,为以后学习循 环小数做铺垫。与此同时,在总结中提升,引领学生经历数学发展的过程,渗透数学学习方法,激发数学学习的兴趣。
顶一下
(0)
0%
踩一下
(0)
0%
上一篇:评刘延革老师“图形的面积”一课
下一篇:“除数是整数的小数除法”教学反思
- 发表评论
-
- 最新评论 进入详细评论页>>