湖南省津市市第二小学   陈克菊

                 

学情分析

在学习了循环小数的基础上，教材安排了本课时内容，有三个方面的作用：一是巩固循环小数；二是熟练计算器的使用；三是探索规律。但教学重心是规律的探索。而学生在一年级时就开始学习找规律，具有一定的探索规律的经验。四年级时又学会了使用计算器来进行四则运算，还经历了“用计算器计算——观察发现规律——利用规律写算式结果”这一利用计算器探索规律的过程，积累了一定的利用计算器探索规律的经验。因此，学生在利用计算器计算、观察发现规律、利用规律写算式结果都不存在困难，但对准确概括表达规律和根据规律续写算式有一定的困难。

 

教学工具

教具：教学课件、计算器。

学具：计算器、学习单。                    

 

教学目标

1.能借助计算器探索规律，并应用规律解决问题。

 

2.在独立思考和交流中培养观察、比较、归纳、推理的思维能力。    

 

3.培养学习数学的兴趣和探索意识。

教学重难点

重点：用计算器探索规律，概括表达规律。

难点：概括表达规律。

 

教学方法

启发谈话法、尝试法、发现法、探究法、练习法、竞赛法、游戏法。

 

教学过程

一、游戏激趣，揭示课题 

（1）谈话导入。

师：这节课你们多带了一样学习工具，是什么呀？

生：计算器。

师：会使用吗？下面我们用它来玩个“猜数”游戏，好吗？请看游戏规则。

（2）“猜数”游戏。

师：（课件出示游戏规则）都清楚了吗？好，开始。（师生同步操作计算）

师：来，你说我猜。你计算器上的显示结果是——？ 

师：你喜欢的数字是……，对吗？ 谁再来试试。（指名3人，师相机板书）

师：想知道我最喜欢的数字是几吗？我的显示结果是×（前面学生未出现的结果），你能猜出来吗？

师：这么厉害，你看出什么了？

生：显示结果是喜欢的数字的9倍，只要用结果除以9就可以猜到了。

师：你们的也符合这个规律吗？看（课件出示算式和结果），难怪结果除以9 的得数就是我们最喜欢的数字。说说，刚开始老师猜中你最喜欢的数字时，你什么感觉？现在呢？

学生说自己的感觉。

师：看，规律多神奇啊！回顾一下刚才的猜数游戏，我们先用——

生：先用计算器计算，再发现规律，最后应用规律推算结果。（板书：用计算器计算——发现规律——应用规律  推算结果）

师：这节课我们就用计算器探索规律。（贴课题）看到这个课题，你想到了哪些问题？

学生提问。

师：来，带着这些问题继续学习。

 

二、自主探索，发现规律 

1. 操作计算。

课件出示：1÷11=        2÷11=        3÷11=

师：用计算器计算，记录在学习单上。比一比，谁算得又对又快？

学生独立计算，师关注进度。

学生汇报。

师：谁来说说计算结果？（学生汇报，师课件配合出示）

师：有不同的吗？

生：第一题，我的计算器上显示的是0.09090909091。

师：怎么回事儿？

生：因为这是一个循环小数，而计算器显示的位数是有限的，所以它默认四舍五入了。

师：循环小数，你怎么知道的？

生：因为小数部分09在依次不断重复出现，这里只重复了5次，原因是计算器显示的位数有限，所以就把最后的数字四舍五入了。如果能显示更多位，一定可以不断重复继续下去。

师：还有不同的想法吗？

生：0.09×11=0.99，0.0909×11=0.9999，都和1相差1个计数单位，所以每次商9后还余1个计数单位，因此结果是一个循环小数。

师：他们说的有道理吗？能用所学的知识做出合理解释，真棒！ 

师：看来，计算器中的规律不少啊！课前，老师也查询了有关资料。（课件出示相关信息）这真是不查不知道，一查吓一跳。

2. 发现规律，推算结果。

课件出示：4÷11        5÷11         6÷11

师：用你喜欢的方式计算，并记录在学习单上。

学生选择自己的方式计算。

师：奇怪，这么快？ 这轮你最快，请你说计算结果。

学生汇报。

师：他的结果和你们一样吗？怎么可能？他根本就没动计算器。

生：我是根据规律推算的。大家看，每一组算式中的除数都是11，被除数是1的几倍，商就是第一个商的几倍。也就是整数部分都是0，小数部分的循环节就是9的几倍。

师：哦，发现规律啦！他发现的规律正确吗？难怪他的答案和大家一样。看，发现规律后推算结果比使用计算器计算还要快。

师：给大家说说，你是怎样观察发现规律的？

生：我先观察相同的部分，也就是除数都是11。再观察有变化的部分，有被除数和商，从上往下观察，后面的被除数是第一个算式中被除数的几倍，商也是第一个的几倍。也就是被除数和商同时乘一个不为零的数。

师：看，先找相同，再找不同，然后分析不同之间的关系，这样观察的确很容易发现规律。还有不同的观察方法吗？

生：我是按顺序观察的。我先从左往右观察算式，发现都有被除数、除号、除数和商。我接着观察被除数，从上往下依次为连续的自然数，再观察除数，都是11，然后观察商，都是循环小数，整数部分都是0，小数部分是两位数的循环节，都是9的倍数，最后整体观察商和被除数有关系，被除数是几，商的循环节就是几的9倍。

师：说的真好，无论是哪种观察方法，都能做到有序观察，方便我们找到数与数、算式与算式之间的联系和变化规律。

师：谁再说说你发现的规律？

生：除数不变，被除数乘几，商的循环节也乘几。

生：除数都是11，商的整数部分都是0的循环小数。被除数是几，循环节就是9的几倍。

师：你觉得哪个规律好？为什么？ 

学生反馈。

师：是啊，不管黑猫白猫，能捉老鼠就是好猫。只要根据你表达的规律能推算结果，就是好规律。

师：它们之间有联系吗？

生：都是先说算式的特点，再说结果的特点。

师：是啊，先说算式特点，再说结果的特点，这样表达规律条理特别清晰。（板书：先算式   再结果）

3.续写算式。

课件出示：根据发现的规律你还能写出哪些算式呢？

师：来，把你想到的算式续写在学习单上。

学生独立续写算式。

指名上台汇报。

师：你们有什么问题想和他交流吗？

生：你是怎样想到这些算式的？

生：因为这些算式中除数都是11，被除数是从小到大排列的自然数，而商的规律和前面一样。

生：你为什么不接着写啦？

生：因为11÷11，如果按照规律得0.9999……，但是11÷11得1，我觉得有问题，所以就没写了。

师：你们也是这样想的？难道我们发现的规律失效了？

师：实际上，我们探索出来的规律并没有失效，只是超出了我们小学的数学知识范围了。当我们继续往后学习你会发现0.99999…真的等于1，有兴趣的课后自己去查阅。（课件出示0.9999…=1）

师：那如果是12÷11、13÷11呢？你还能推算出它们的结果吗？

指名汇报。

师：现在你有什么想法？

指名学生说想法。

师：是啊，数学很奇妙！你们很厉害！不仅能合理使用计算器，还能发现规律，应用规律推算得数和续写算式。为你们点赞！ 

三、巩固应用，拓展提升

1. 牛刀小试。

师：学以致用！来，看题。

课件出示：用计算器计算前三题，试着写出后两题的积。

                 3×0.7       =

                3.3×6.7      =

               3.33×66.7     =

              3.333×666.7    =

             3.3333×6666.7   =

你能用发现的规律接着写出下面一个算式吗？

师：谁来读题？

指名读题。

师：明白要求吗？比一比，谁完成得又对又快？

学生独立完成在学习单上。

师：谁来分享一下？

学生上展台汇报。

师：你们有什么问题想和他交流吗？

生：这组题的规律是什么？

生：两个因数中有几位小数，积中整数部分就是几个2、小数部分就是几个1。（说法不唯一）

生：你是怎样找出规律的？

生：我先观察被乘数和乘数，从上往下的变化规律是…，而积的变化规律是…，所以我发现的规律是…

生：你能写出多少个这样的算式？

生：写不完。因为只要第一个因数的整数部分是3，小数部分是几个3，第二个因数的整数部分是相同个数的6，小数部分是7，它们的积的整数部分就是比几多1个2，小数部分就是比几多1个1。

师：同学们，他们的交流怎么样？

生评价。

师：数风流人物，还看今朝！你们的交流和评价真是一道亮丽的风景！掌声送给自己！

师：回顾一下，刚才我们是怎样完成这类题的？

生：先用计算器计算几个算式，再观察发现规律，接着用规律推算出得数，最后用规律续写算式。（板书：续写算式）

师：学习到这儿，你有怎样的思考？

生：只要是用计算器来探索规律，都可以用这样的探究方式来进行探索。

生：只要是探索规律，就可以先计算，再观察发现规律，利用规律写结果，也可以根据规律续写算式。

生：道道使用计算器速度反而慢，合理使用计算器，发现规律后直接推算出结果，又快又正确。

……

师：千金难买回头看，咱们这一回头，居然积累了这么多经验，真棒。

2. 大显身手。

师：同学们，在数字王国里有一些神秘的数，据说发现于古埃及的金字塔内，它们就藏在下面算式的结果中。有信心找到它们吗？ 

课件出示：

 用计算器计算。 

  1÷7=                                                     

  2÷7=                                                                   

  3÷7=                                                                   

  4÷7=                                                

不计算，直接写出得数，再用计算器验证。

  5÷7=                 

  6÷7=                      

（1）四人小组合作完成练习。

师：来，三人小组合作，并做好分享准备。（巡视中：想一想，怎样简洁清晰地介绍自己的想法，让同学们都听明白。）

小组合作。

（2）全班汇报。

师：哪个小组来和大家分享一下？

全班交流。

师：你们有什么问题想请教和交流的吗？

生生互动。

（3）介绍“142857”。

师：同学们，现在你知道这些神秘的数是谁了吗？没错，它就是142857。（课件出示142857）人们又叫它走马灯数（课件出示圆圈图），它的1~6倍，都恰好是这六个数字的重新排列，并且是按次序排列的哦，看，是不是很像“走马灯”呢？有人说它是世界上最神奇的数（课件出示算式图），课后同学们可以去进一步了解它更多的神奇之处。

（4）回顾反思。

师：做完这题有什么经验？

指名汇报。

师：看，玩转规律窍门多，凝心聚力办法多。

3.勇攀高峰。

师：同学们，看过《攀登者》吗？中国登山员们用自己的勇敢和无畏向世界证明珠穆朗玛峰是中国的国土！今天，老师也希望你们今天能勇攀数学高峰，有信心吗？

课件出示：

计算：22222222×55555555=

（1）交流做法。

师：你们准备怎么算？

生：用计算器计算。

师：好，那就赶快行动吧。

学生发现用计算器解决不了。

（2）引导思考。

师：同学们，想到办法了吗？

生：我们可以先退回去，从几个简单易算的式子开始，说不定就会发现规律，再运用规律就能写出结果了。

（3）从简开始，化解困难。

生说算式，师课件出示：

2×5=10  

22×55=1210

222×555=123210

师：有能直接写出结果的同学了吗？如果不行，可以再写几个算式试试。

指名汇报。

师：同学们，做完这题你有什么想法？

生：当我们遇到困难时，可以从简单容易的地方入手，发现规律，运用规律就能帮助我们解决难题。

生：当我们遇到困难时，不要轻易放弃，发挥团队的力量，也许会有“柳暗花明又一村”的时候。……

师：我国古代思想家老子教导我们，来，一起读：“天下难事，必作于易；天下大事，必作于细。”（课件出示）知道什么意思吗？

生：天下所有的难事都要从容易的地方开始，天下所有大事都要从细致的地方开始。

师：没错，从简开始，便能化解困难！（板书：从简开始）

四、课堂小结

师：通过这节课的学习，你最大的感受是什么？还有什么疑问吗？ 

师：同学们，学无止境，还有更多有趣的规律等着我们去探索呢！

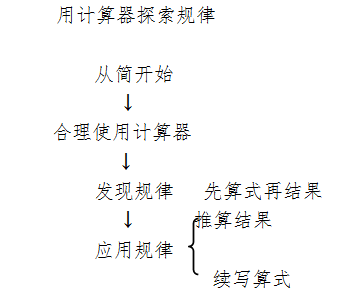
五、板书设计