“分数加减法练习”教学思考与实践

巧借九宫之奥妙 破解练习之枯燥
—— “分数加减法练习”教学思考与实践
● 课前思考
要参加一项课堂教学评比,内容指定为人教版《数学》五年级下册“分数加减法练习”。
面对这样一个主题,我们把思考的重点放在“怎么练”上。
之所以要重点思考“怎么练”,是因为本课练习的内容相对而言比较清楚——分数加减法;更为主要的原因是练习课枯燥,学生不感兴趣(在计算类的练习课上表现得尤为突出)。
仔细分析后认为,本课要破解练习的枯燥,激发学生练习的兴趣,必须在练习的形式上有所创新。
思虑再三,我们选择“九宫”作为本节课练习的载体,以求突破。
首先,九宫起源于“洛书”这个神话故事,蕴含着奥妙无穷的数学内涵。因此,用神话故事引入,巧借九宫的奇妙,能在一定程度上引起学生的学习兴趣,激发学习的积极情绪。
其次,“洛书”中的九宫用1~9九个自然数填写,看似简单,实则奇妙。
本节课,我们将“洛书”作为基础模型,通过“1~9作分子,分母都为10”和“1~9作分母,分子都为1”两次变化,以“猜一猜变化后的九宫是否依然成立”为任务驱动,激发学生运用计算进行探索的欲望,进而实现使学生积极主动地进行分数加减法计算(练习)的目的。
最后,依托两次变化,融合“口算”“笔算”和“估算”。
第一次变化,是相对简单的同分母分数相加减,适合口算;
第二次变化,涉及异分母分数相加减,自然适合笔算;
在第二次变化时判断能否成为九宫图的过程中,除了笔算,估算也可行。
计算“三宝”灵活运用,互为补充,各显优势。
● 课堂实践
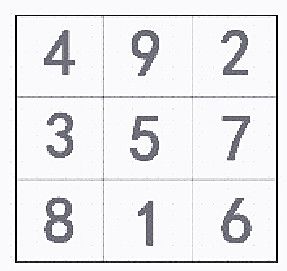
课前教师以“洛书”为载体与学生进行交流,使学生了解“洛书”的神话传说,同时认识“九宫图”的特点——8个和都相等。
一、探索同分母分数九宫图
1.第一次变化:原数作分子,分母为10
师:这节课,我们继续来研究这幅“九宫图”(下图)。现在,老师要对这幅九宫图进行变化了,请注意观察。
课件演示:先把4变成 4/10,再把9变成 9/10。
师:猜一猜,2会变成多少呢?
生(齐):2/10。
师:下面这些数呢?
随着学生的回答,依次完成其他数的变化,形成下图。
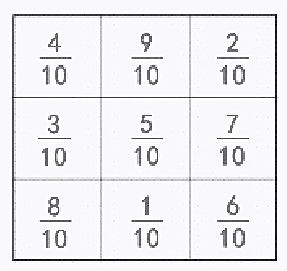
2.验证变化后的图是否还具有九宫图的特征
(1)质疑:用九宫图中原来的数作分子,分母都是10,还符合8个和相等的特征吗?
(2)学生独立观察。(口算)
(3)反馈学生的想法。
生:成立的,因为现在每行、每列,还有斜角的和是一样的,我算过了。
根据学生的回答,教师板书第一行:4/10+9/10+2/10=15/10=3/2,并和学生一起口算验证其他7个和也都是3/2。
(4)结论:用九宫图中原来的数作分子,分母都是10,仍然具有九宫图的特征。
3.用其他数作分母行不行
师:用原来的数作分子,分母都是10,这个九宫图依然符合要求。如果把分母换成别的数,行不行?
(课件出示下图)
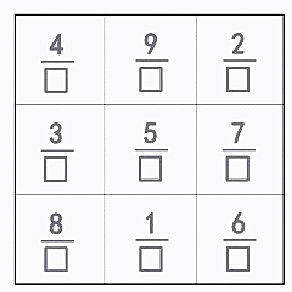
(1)学生在空白九宫图上独立尝试。
(2)反馈学生的尝试。
先展示几位学生的尝试,并解释是否成立(教师根据学生的解释板书第一行算式);
再请几位学生讲清楚分母用了几,是否成立。
4.为什么只要用原数作分子,分母相同,九宫图依然成立
师:你们的尝试都成立,有什么想法?
生:我认为,只要用原来的数作分子,分母是相同的数,就可以写出无数种方法。
师:你讲得很有道理。不知道你有没有想过,这是为什么呀?先自己想一想,然后同桌交流。
生:我发现,不管分母怎么变,分子加起来永远是15。
师:这说明什么?
引导学生逐步认识到:改变分母,只是在改变分数单位的大小;分子不变,分数单位的个数一直没有改变。所以,不管分母怎么变(适当提醒:分母不能为0),永远符合原来九宫的要求。
二、探索同分子分数九宫图
1.第二次变化:原数作分母,分子为1
师:刚才我们研究了用九宫原来的数作分子,只要分母相同,依然符合九宫的要求。想一想,还能怎么变?
老师想到一种新的变化形式,请看。
(课件出示下图)你能看懂吗?
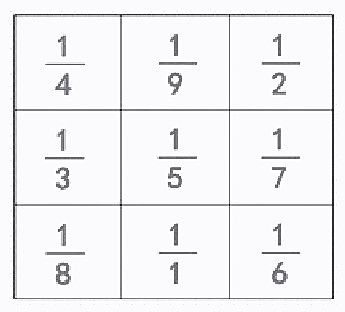
生:分子都变成了1。
生:分母不再是相同的数了。
生:我发现,分母就是原来整数九宫的那些数。
师:这次老师把九宫原来的数都变成了分母,分子统一是1。
2.验证变化后的图是否还具有九宫图的特征
(1)质疑:这样变化之后,还符合8个和相等的特征吗?
(2)学生观察。
(3)学生独立计算(笔算),验证自己的想法。
(4)反馈学生的验证。
生:不符合,第一行的和是31/36,第二行的和是71/105。
师:他计算了两个和就得出结论,你们同意吗?
生:同意。只要有2个和不相等,就说明不符合8个和都相等的要求。
生:我也是这样想的,我计算了第一列和第二列,和分别是17/24和114/45,所以也发现是不行的。
此时有些学生在抱怨:原来算两个和就可以了,我都白算了。
师:这两位同学通过计算发现,8个和不再相等,所以不符合要求了。其他同学的验证结果如何?
生(众):不符合要求。
师:刚才我们通过计算(笔算)发现不符合8个和相等的要求,还有不一样的方法吗?
生:我发现第一行1/4+1/9+1/2 的和小于1,而第三行1/8+1/1+1/6的和一定大于1,所以这两行的和不相等,就知道不符合要求了。
师:为什么第三行不计算也知道大于1?
生:中间1/1就是1,再加上两个数,和一定大于1。
师:让我们把掌声送给他。他先观察了这些数的特点,然后通过估算得出结论。
3.基于第二次变化换数,形成新的九宫图
(1)讨论换掉的数。
师:通过计算发现,如果用原来的数作分母,分子都是1,就不符合九宫8个和相等的要求了。那么,如果我们把其中的几个数换掉,能不能使它符合九宫图的要求呢?
师:你最想换掉谁?
生(齐):1/1。
师:为什么?
生:它太大了。
师:好的,只换掉1/1够吗?
生:不够。
师:现在去掉其中的5个数,留下这样的4 个数(下图),你觉得行了吗?
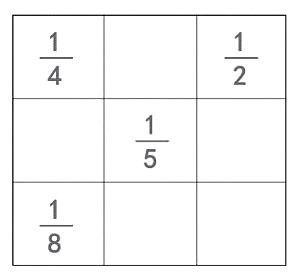
生:试试看吧!
(2)学生计算填写。
师:仔细观察这幅图,你会算哪一格?
生:我会算第一行中间的数。
生:我会算第一列中间的数。
师:怎么算第一行中间的数呢?
生:斜的三个数可以算出一个和,用这个和减去第一行中的两个数,就能算出中间的数了。
学生计算后得到第一行中间的数是3/40 ,然后计算第一列中间的数,得到 9/20 。
(课件出示数据)
师:我们已经填出了两个数,剩下的三个数请同学们独立计算。
(3)反馈。

师:我这里有两位同学的结果,有和第一幅图相同的吗?
(有)
有和第二幅相同的吗?
(有)
师:那就奇怪了,哪个是对的呢?我们来听听他们的算法。
两位学生分别介绍自己得到3/8 和3/20 的计算方法,一个斜着算,一个按列算。
师:看来,计算方法都正确,那它们符合8个和都相等吗?
学生通过计算发现,这两个结果都不能满足8个和相等的要求,因此都不对。
三、第二次换数,沟通前后两次变化
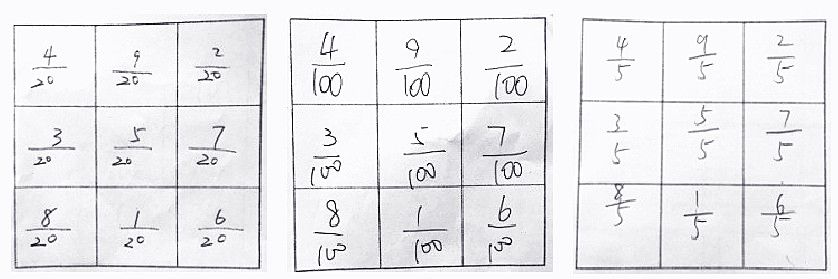
师:看来,用这样的办法是行不通的,原因是我们换的数不对。刚才大家一致认为要把1/1换掉,其实1/1是不能换掉的,这叫“置之死地而后生”。
课件出示新的换法(下面左图),学生静静观察后告知这样还是不行,接着变换数的位置 (下面中图)。
师:现在这4个数一定行了。你看出来了吗?
(学生困惑)
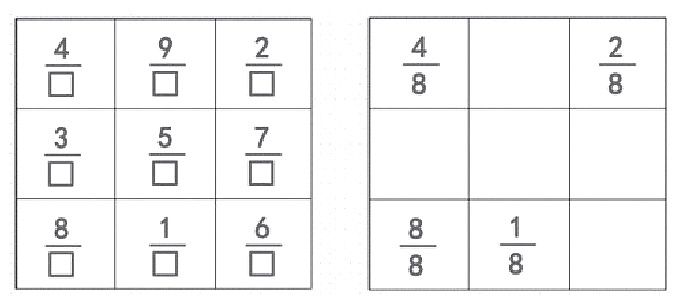
师:老师再把这些数都化成分母是8的分数(下面右图),现在你看出来了吗?
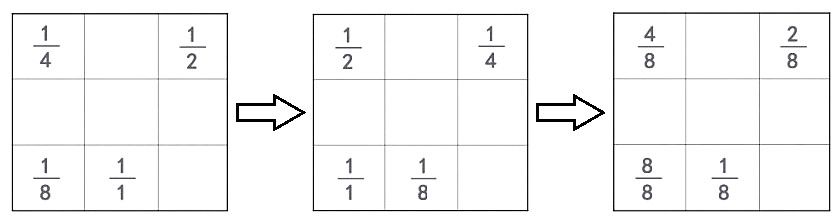
生:看出来了。
师:请你在草稿本上写下来吧。
生:这是我的填法。
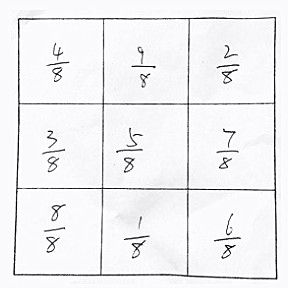
师:看了这位同学的九宫图,你有什么想说的?
生:这又回到了刚才的情况,分子是原来九宫的整数,分母变成了相同的数字8。所以,这个九宫图具有8个和相等的特征。
(教师配 合出示课件,学生表示惊讶)
师:你讲得真好!是呀,数学有时候就是这么奇妙!
● 后记
课,获得了一等奖。这无疑是对我们本课“形式创新”的肯定。
课堂上,学生的学习是投入的,看不到他们对计算的厌烦,看到的是他们努力通过计算寻找答案的积极探索。
这让我们进一步感受到了创新形式、关注学生学习积极情绪的重要性。
这一次尝试带给我们成功的喜悦,也带给我们深深的思考:如何让学习真正成为快乐的探索?这还需要我们不断摸索。
愿与大家一起 为此而努力!
顶一下
(0)
0%
踩一下
(0)
0%
- 发表评论
-
- 最新评论 进入详细评论页>>