“运算律”课堂教学实录

教学内容
苏教版《数学》四年级下册第55~56页例1、第56页练一练以及第58页练习九第1~3题。
教学目标
1.经历探索加法交换律与结合律的过程,借助几何直观理解并掌握加法交换律与结合律,感知加法交换律与结合律的内在一致性,发展应用意识。
2.在尝试使用符号、字母来表示加法运算律的过程中,培养归纳、概括的能力与符号意识,发展抽象思维能力。
3.能够根据不同运算之间的联系进行合理猜想,培养善于推理和主动研究数学的意识。
课堂实录
一、揭示课题,明确任务
师:你知道什么是“运算律”吗?
生:运算律就是关于运算的规律。
师:“运算律”即运算的定律、规律。我们已学过哪几种运算?
生:加法、减法、乘法、除法四种运算。
师:除了已学过的四则运算,以后我们还会学习其他运算。今天,我们先来研究加法的运算规律。(板书课题:加法运算律)
二、探索规律,理解规律
1.发现交换律
师:在研究加法的运算规律之前,我们先来口算几组题目。(下图)想一想,这四组算式有什么特点,你有什么发现?

生:每组的两道题两个加数相同,只是调换了位置,结果是一样的。
师:结果相同,说明每组的两个算式的和相等。所以,可以把两个算式合并为一个等式, 例如,3+4=7和4+3=7可以写成3+4=4+3。你也能把另外三组算式写成等式吗?(学生口答)

师:你还能照样子再写几个这样的等式吗?
(学生列举,教师板书)
师:这样的等式可以写出多少个?
生(众):无数个。
师:你发现加法有什么规律?你能给它取个名字吗?
生:加法中,调换两个加数的位置,结果是相等的。我知道这个规律叫加法交换律。
(师板书:两个数相加,交换它们的位置,和不变。——加法交换律)
2.概括交换律
师:加法交换律的等式我们可以写出无数个,但也可以只用一个等式就能把所有这样的等式都表示出来,你能创造出这样的等式吗?
生:一个加数+另一个加数=另一个加数+一个加数。
师:用文字来概括,好办法。但是,数学讲 究简洁明了,还能更简单些吗?
生1: 甲+乙=乙+甲。
生2: ■+▲=▲+■。
生3: a+b=b+a。
师:像这样用含有文字、图形或字母的等式来表示加法交换律一目了然,这里的甲、乙分别可以代表哪些数呢?■与▲呢?a、b呢?
生:它们都代表两个不同的数,整数、小数、分数都可以。
师:无数个等式能合并成一个等式,很神奇。一个符号或字母能代表若干个不同的数,含有字母、符号的等式表示运算规律简单清楚。数学上通常用a+b=b+a来表示加法交换律。
3.解释交换律
师:生活中我们会经常碰到一些加法的问题,解决问题时常常可以用交换律的方法。谁能举例说一说?
生1:我们班有26名男生,25名女生,26+25或者25+26都是求全班的总人数。
生2:成语故事“朝三暮四”讲的也是交换律的故事,3+4=4+3。
师:你知道成语中也有交换律,真了不起!我们还可以用线段图来解释我们的发现。(下图)家、少年宫、商店在一条线段上,家 到少年宫的距离是a米,少年宫到商店的距离是b米,这里可以列出哪两个不同的加法算式?

生:a+b和b+a。
师:如果你走在这条路上,第一个加数表示你先走的那一段,能看出这两个算式分别表示的走法吗?
生:a+b表示从家出发先到少年宫,再走到商店,b+a是反方向走的。
师:从不同的地点出发,向不同的方向走,起点与终点互换了一下,都是同一条路,所以总路程是相等的。这个线段图非常直观形象地解释、证明了加法交换律。
4.拓展交换律
师:如果家、少年宫、商店的位置不在一条线段上(下图),家与少年宫的距离是a米,少年宫与商店的距离是b米,商店与家之间的距离是c米,你从一个地点出发,沿着这三条路走一圈,一共走了多远?能列出哪些加法算式呢?
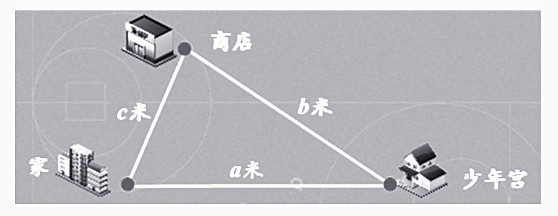
生1:从家到少年宫,然后到商店,最后回到家, a+b+c。
生2:也可以从少年宫出发,先到商店,接着走到家,最后回到少年宫,b+c+a。
生3:先从商店出发到家,再去少年宫,最后回到商店,c+a+b。
生4:也可以把他们三个人的走法反过来,第一种走法是c+b+a,第二种走法是a+c+b,第三种走法是b+a+c。
师:(板书6个加法算式)这6个算式都相等吗?
生(众):相等。
师:为什么?
生:这些算式都是求总路程,也就是这个三角形的周长。
师:看来,三个数相加也有交换律,那四个数、五个数呢?
生:只要是连加,无论几个加数,交换它们的位置,和不变。好比我们求四边形、五边形的周长一样,可以从任何一条边的长度加起。
师:看来,规律的内容应改成——几个数相加,交换加数的位置,和不变。
5.推导结合律
师:在a+b+c=b+c+a这个交换律的等式中,前一个算式a+b+c中,我们先算的是哪两个数的和?后一个算式b+c+a中,我们又是先算哪 两个数的和?
生:前面的算式先算a+b的和,后面的算式先算b+c的和。
师:改变了加数的位置,计算的顺序随之改变了,但和是不变的。如果我们不改变加数的位置,能不能改变计算的顺序呢?也就是在a+b+c=b+c+a这个等式中,怎样才能实现先算划线的部分,你想到了什么办法?
生:把划线的部分加上括号就行了。
师:括号是改变运算顺序的数学工具,所以只要在划横线的部分添上括号,计算时就要先算括号里的,这是我们已经掌握的数学知识。a+(b+c)其实跟b+c+a在图中行走的方法相同,这种不改变加数的位置,通过添加括号改变计算顺序保 持结果不变的规律就是加法的结合律,用字母公式表示就是(a+b)+c=a+(b+c)。【板书:(a+b)+c=a+(b+c)——加法结合律】谁能说一说这个等式表示的意思?
生:三个数相加,可以先把前两个数加起来,也可以先把后两个数加起来,结果相等。
6.验证结合律
师:把结合律这个等式中的a、b、c换成具体的数算一算,看看是否真的相等。
(学生举例,教师板书)
师:从刚才的学习中我们发现,几个数连加的交换律、结合律其实是用不同的方法来改变计算的顺序,本质上是相同的,只是方法不同。(下图)

三、梳理应用,联想推理
1.梳理回顾
师:今天你有什么收获?
(学生交流)
师:回想一下,过去我们曾经在哪儿用到过或见到过加法的运算律?
生1:加法竖式计算,验算时交换加数的位置,用到了交换律。
生2:一年级学习数的拆分,比如,5可以分成4和1,也可以分成1和4,用的也是交换律。
师:运算律还能使计算变得简便,以后我们会进一步学习和探究。
2.应用练习
(略)
3.联想推理
师:举例说明加与减、乘与除之间有什么关系。
生1:比如,3+2=5可以变成5-3=2,5-2=3,加法和减法好像是相反的运算。
生2:乘法和除法也是相反的运算。
师:相反的运算数学上称为逆运算,“逆”就是相反的意思。那你知道加与乘、减与除之间的关系吗?
生:加法可以变为乘法,比如,7+7+7可以变成3×7或者7×3。
师:乘法是由相同加数的加法发展而成的一种运算,其实除法与减法的联系也很密切。根据这样的关系,加法有交换律和结合律,你认为其他运算中有可能存在这样的规律吗?
生1:可能都有这样的规律。
生2:我觉得乘法有这样的规律,因为乘法就是相同数的加法。
师:敢于猜想很好,但还要想办法来证明自己的猜想。课后大家可以继续研究。
顶一下
(0)
0%
踩一下
(0)
0%
上一篇:三角形内角和教学思考
下一篇:“运算律”教学课前、课后思考
- 发表评论
-
- 最新评论 进入详细评论页>>