乘法分配律是小学阶段非常重要的学习内容。
    由于它的变式很多，方法灵活，因此一直都是学生容易出错的内容。
    特别是到了六年级，随着数域的扩展，出现小数、分数的乘法分配律时，学生仍然频频出错。
    到底乘法分配律难在哪里？如何突破难点？

    ● 错例诊断

    【错例1】凑整思想的僵化，造成生搬硬套
 

 
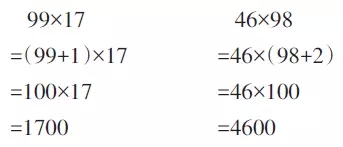
    诊断分析：从这两个错题可以看出，学生片面关注99和98“接近整百数”的特点，没有考虑到整个算式的结构，没有准确分析“这个数”在算式中与其他数之间的运算关系，只是盲目进行凑整，必然造成计算过程前后不等价。

    【错例2】算理理解不到位，造成丢三落四
 

 
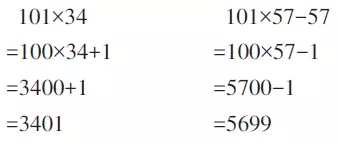
    诊断分析：这种“漏项”的现象十分普遍。遇到“1乘公共因数”的情形时，学生没有自觉地把“1个几”或者“几个1”用乘法算式表示出来，造成计算过程中的疏漏。
    究其原因，还是对乘法的意义掌握得不扎实。

    【错例3】乘法分配律和乘法结合律的混淆，造成过程混乱
 

 
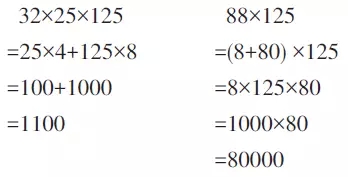
    诊断分析：这里明显出现了算理与算法的脱节。学生未能真正辨析和理解乘法结合律与乘法分配律在意义和形式上的区别，于是在解题时思路特别容易受表面形式的干扰，片面考虑凑整，造成运算定律的误用和运算过程的混乱。

    【错例4】重形式记忆轻算理理解，造成计算循环
 

 
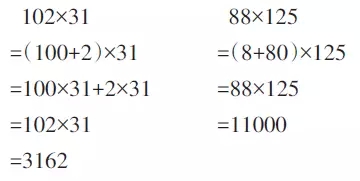
    诊断分析：学生在做第一步时，思路是清晰的，把102看成(100+2),把88分解成（8+80），第二步就应用乘法分配律进行等价变形，本来是顺理成章的事情，但是在第三步时又“鬼使神差”地回到了原题上。
    说明学生仍然停留在运算定律形式上的套用，这显然是单纯注重形式记忆造成的。

    ● 实践反思

    学生出现上述四种错误的根本原因在于不理解算式的意义，仅仅停留在题目结构层面上，也就是先找相同的因数，再套用字母公式，不能按照算理正确地思考简算过程。
    笔者认为，教师应从最朴素的算理——乘法的意义出发，坚持“算理先行、理到法随”的教学原则，分析学生的“痛处”，抓住问题的本质，才能对症下药。

    1. 画图明理，帮助学生建立模型画图能够非常直观地反映运算规律

    学生在学习乘法的意义之初，能够通过横着看和竖着看说出图意并列出两个乘法算式。这些经历为进一步研究乘法分配律做好了知识和经验上的准备。
    因此，我们按照“看图想算式——看算式画图——看算式想象—看算式说意义”的步骤帮助学生理解算理，构建乘法分配律的思维模型。

    第一步：看图想算式
    出示：

 
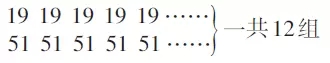
    师：你能说说这幅图表示什么意思吗？（生答略）要求一共是多少，你能想到几种算法？
    生1：横着看，第一行表示12个19，第二行表示12个51，列式是19×12+51×12。
    生2：竖着看，第一组表示19+51的和，一共有这样的12组，列式是（19+51）×12。
    师：同桌两人各选一道算式，算出结果后对比，你发现了什么？
    生：两个算式相等，也就是19×12+51×12=（19+51）×12。
    师：你能试着用自己的话说说这个等式的意思吗？
    生：12 个19 加12 个51，就等于12 个（19＋51）的和。

    一个简单的示意图，直观地再现了算式的意义。
    学生通过横着看、竖着看，自然地将这个等式与乘法的意义联系起来，还能从乘法意义的角度理解左右两边的算式为什么相等。
    经过几组这样的练习，学生看着图就能够得出乘法算式，并说出算式的意义，进一步在理解算理的基础上发现定律，避免从形式上机械记忆。

    第二步：看算式画图教师给出算式，学生根据自己的理解画出示意图
    重点提问：横着看表示什么？竖着看表示什么？几个几加几个几等于几个几？这是第一步的逆向思维过程，目的是通过图式对应，进一步强化意义。

    第三步：看算式想象出示算式，如（15+25）×4，请学生闭上眼睛想一想：图是什么样的？还可以怎样算，为什么？借助想象，让乘法的意义铭刻于心，进一步巩固乘法分配律的算理。

    第四步：看算式说意义
    出示一组算式，如下：

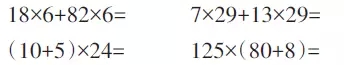
    通过这样一组练习，让学生逐渐脱离画图，看到算式能够马上想到意义，进而顺利写出右边的算式，达到再次巩固算理的目的。

    第五步：总结规律提问：你发现了什么规律？能用一个字母式子表示你发现的规律吗？通过师生互动，引导学生口述规律，并用符号表述规律，初步建立乘法分配律的模型。

    2. 链接旧知，沟通知识之间的内在联系三年级学习过两位数乘一位数

    如12×3，口算时先算10×3=30，2×3=6，再算30+6=36；用竖式算时，求3个12是多少就是求3个10与3个2 的和。
    四年级学过两位数乘两位数，如24×12，即求12个24是多少，等于12个20与12个4的和，列式为（20+4）×12=20×12+4×12。
    进一步让学生思考：四年级学过的三位数乘两位数的竖式（下图），是不是也符合这个规律呢？

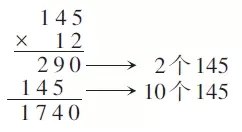
    顺着前面的思路，学生很快得出：145×12就是求12个145是多少，等于2个145加上10个145，即145×12=145×10+145×2。
    通过链接旧知，唤醒学生的已有经验，有效巩固了乘法分配律的算理和算法。

    3. 分层练习，引导学生灵活运用定律

    （1）基本练习，熟悉定律
 

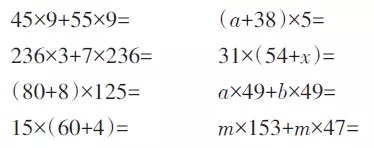
    学生在练习第一组算式之后，会得到这样的经验：相同的因数无论放在乘号前还是乘号后，只要符合“几个几加上几个几”的意义，就能够借助分配律进行等价转换。
    第二组算式都是含有字母的形式，意在通过拓展应用，帮助学生进一步巩固乘法分配律的结构模型。

    （2）对比练习，积累经验
    ① 乘法结合律与乘法分配律的对比有时，乘法结合律和乘法分配律可以适用于同一题，只是拆法有所不同。简单地说，拆成两数之积就是结合律，拆成两数之和就是分配律。例如：

    ② 对比相似题，选择合适的计算方法

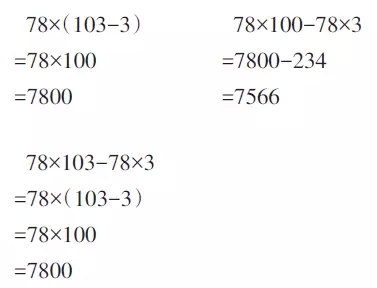
    通过这一题组的对比，让学生明白，具体问题要具体分析，有些题目按照运算顺序直接计算就已经很简便了，有些题目则需要使用运算定律才能使计算简便。

    ③ 同题对比，优化简算的方法
    第一组：

    第二组：

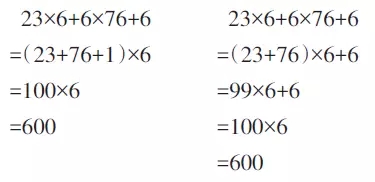
    学生在进行简算时往往存在思维水平上的参差不齐，这是一个普遍现象。
    教师要善于通过不同解法的对比，促进学生自觉优化方法，逐步提高简算水平。

   （3）提高练习，拓展延伸
    ① 108×9+91×9+9   ② 48×25   ③ 26×17+13×66
    第①题是由两个因数拓展到三个因数。
    第②题可以有不同的解题思路：既可以把48拆成（40+8），直接运用乘法分配律简算；又可以把48拆成6×8或者4×12，用乘法交换律和结合律来简算。
    第③题有一定的难度，看上去没有明显的符合规律的结构，但是如果把26拆成13×2，问题就迎刃而解了。

    总体来说，第一层是最基本的结构训练，所选题目都与运算定律完全一致，目的是让学生熟练掌握定律。
    第二层是简单变式，通过对比练习，让学生明确乘法结合律与分配律的异同，学会根据数据特点选择并优化计算方法。
    第三层是拓展提高，这类题目需要经过两次或两次以上的变形，才能转化成基本题。
    无论题目怎样变化，只要学生按照乘法的意义去思考，就一定能找到解决问题的突破口。

    4. 潜移默化，培养学生的数学素养

    在研究了乘法对于加法的分配律之后，教师可启发学生进一步思考：除了乘法对于加法的分配律，你还能想到什么？
    这个看似简单的问题一下子激起学生内心的涟漪，他们自然地想到：乘法对于减法有没有分配律呢？乘法对于除法呢？……
    有了猜想就需要进一步的证明，教师“顺水推舟”，让学生在小组内举例验证。
    这个环节看似微小却意义深远，既打开了学生的思路，又有助于培养学生良好的思维品质和严谨的研究态度。
   （《小学数学教师》2016年第3期）

    （重庆市大渡口区钰鑫小学 彭志秀老师推介）