“图形的面积”教学实践与思考

抓住度量本质 串联面积教学
——“图形的面积”教学实践与思考
度量包含“度”和“量”两个方面,“度”是度量单位,“量”是测量;表示测量结果的数,叫做数量。面积就是用单位面积测量出的结果,它是一个数量。而教师在面积内容的教学中,往往更重视面积计算公式的获得和应用,忽略了度量本质的体现,更忽视了二维图形的大小需要两个维度的数值来刻画的特点。“图形的面积”一课,以平行四边形为纽带,串联起整个平面图形面积的计算,突出度量的内涵,凸显面积计算的特点。
一、直接引入,揭示课题
师:同学们,今天我们来研究图形的面积。谁能说一说什么叫面积?
生:面积就是一个黑板面的大小。
……
师:对,生活中物体的表面的大小、数学中图形的面的大小叫做面积。今天就来研究数学中平面图形的面积。
二、回忆旧知,发现规律
师:同学们都认识哪些平面图形?
生:正方形、长方形、圆形、平行四边形、三角形、梯形……
师:在这些图形中,你们已经学习了哪些图形的面积计算方法?
生:长方形的面积等于长乘宽。(板书:S=长×宽)
生:正方形的面积等于边长乘边长。(板书:S=边长×边长)
师:求长方形面积的时候,长表示什么意思?宽表示什么意思?(生沉默)
师:回忆一下,面的大小是用单位面积量出来的。长是5表示一行有5个单位面积,如果长是8,表示一行有8个单位面积。现在再思考一下,长表示什么意思?宽表示什么意思?
生:长表示一行有几个单位面积。
生:宽表示有这样的几行。
(教师相机出示下图)
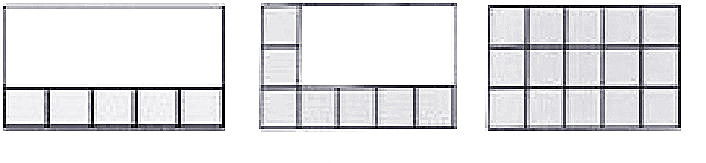
师:一行5个乘3行,得到的15个单位面积就是这个长方形的面积。再思考一下,正方形的面积计算公式“边长×边长”中,两个“边长”的含义是什么?

生:第一个“边长”表示一行有几个单位面积,第二个“边长”表示有这样的几行,相乘求出一共有多少个单位面积。(出示右图)
师:长方形和正方形的面积计算方法有什么相同的地方?
生:都是用一行单位面积的个数乘这样的几行。
(板书:S=每行单位面积的个数×行数)
【设计意图:对长、正方形面积计算方法的回忆,一是让学生深刻体会面积是用单位面积刻画的,单位面积的多少代表了图形的面积;二是让学生初步感受二维图形的面积是由长和宽两个维度的量相乘得到的。】
三、创设冲突,引发猜想
师:能用“每行单位面积的个数×行数”的方法求这些图形(出示圆、平行四边形、三角形、梯形)的面积吗?
生:(坚定地)不可以。
师:说说理由。
生:梯形不行,它有一条边是长的,有一条边是短的。
生:圆形不行,它没有长和宽。
生:三角形也不,三角形只有三条边,长方形和正方形都有四条边。
生:平行四边形也不行,它的四个角不是直角。
师:如果这些图形中有的可以用这个方法计算,你觉得最有可能是哪个图形?
生:平行四边形!们就来研究一下,平行四边形能不能用这样的方法求面积。
【设计意图:由于平行四边形、三角形、梯形、圆外形上不像长、正方形那样方方正正、直上直下,直观感觉上不能用两个量相乘得到单位面积的个数,这就引发了学生的猜想。学生在寻找这些图形与长、正方形的不同之处时,也为后面的转化做好了准备(不顺之处即转化之处),冲突也引发了探究的需求。】
四、动手操作,探索发现
师:每位同学有一个印有平行四边形(形状、大小都不同)的透明片,请你们借助方格纸测量平行四边形的面积(一格是1平方厘米),看看在数的过程中能不能发现规律。
(学生动手操作,数平行四边形的面积,教师巡视)
师:我们交流一下,你是怎么数的?
生:将不满一格的部分平移凑成整格,每一行都可以这样凑成整格。 (下图)

师:两侧不满整格的部分都可以拼成整格吗?观察一下,现在每行单位面积的个数有怎样的规律?
生:每行都可以凑成整格,每行单位面积的个数是一样的!
师:这个平行四边形的面积是多少?怎么算?
生:5乘3等于15。用一行单位面积的个数乘行数。
【设计意图:对于平行四边形面积的探索,教学时并没有急于进行图形转化,而是让学生用方格纸上的单位面积去量,通过测量得到单位面积的个数,继续渗透度量的本质。在测量的过程中,学生本能地将不满整格的部分拼成整格,转化方法自然浮出水面。】
师:再看下一位同学是怎么解决的。
生:我把左边三角形的部分切下来,移过去和右边对齐。(教师辅助圈画)
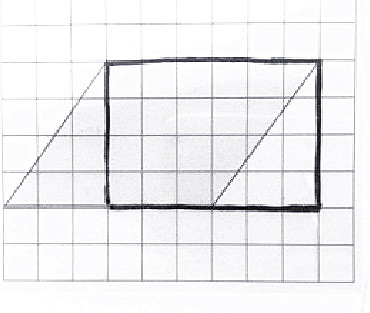
师:将左边的三角形平移到右边,这个图形变成了——
生:长方形。
师:长方形的面积怎么求?
生:长乘宽!每行单位面积的个数乘行数!
师:不同方法都说明,平行四边形的面积可以用每行单位面积的个数乘行数得到。那么,每行单位面积的个数对应平行四边形的什么?行数又对应着什么呢?
生:每行单位面积的个数就是底。
生:行数就是高!
师:对照着图看一看,底表示一行有多少个单位面积,高表示有几行,每行单位面积的个数乘行数时,实际就是谁乘谁?
生:底乘高!(板书:S=底×高)
【设计意图:将平行四边形转化成长方形进行研究的过程中,师生始终在方格图的环境下进行观察和思考,一是体现单位面积的密铺,二是让学生清晰地感受每行单位面积同样多,为总结平行四边形的面积可用“每行单位面积的个数×行数”来计算做好直观支撑。】
师:两种方法有什么相同和不同之处?
生:相同之处是,两种方法都把图形进行了割补。不同之处是,第一种方法是一格一格拼凑完整的;第二种方法是将一整块平移过去,拼成一个长方形。
师:说得真好!相同之处是两种方法都把图形进行了转化,转化的过程中图形的大小变了吗?(没有)但转化后图形中的角都变成了(直角),这样计算平行四边形的面积就可以使用这种面积计算方法了。不同之处在于,一种方法是将不整格的拼成整格的,把不整齐转化成整齐(板书:不整齐→整齐),另一种方法是把一整块移过去,将平行四边形变成长方形(板书:新知→旧知)。两种方法都说明平行四边形的面积可以用“每行单位面积的个数×行数”的方法计算得到。
【设计意图:在探讨平行四边形面积计算方法的过程中,学生只是本能地运用了转化。为了清晰地认识转化的方法,感受转化的价值,在总结完平行四边形面积计算方法之后,教师展开了对解决问题方法的讨论,让学生认识到什么是转化方法及转化的不同方式。学生从无意识地应用到有意识地注意,积累了转化经验。】
师:接下来,请同学们做几个练习。先独立思考,再交流汇报。
练习1:
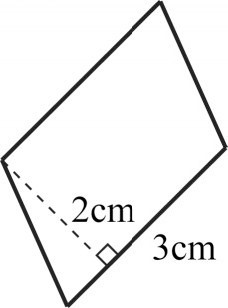
师:3表示什么?2表示什么?面积是多少?
生:一行有3个单位面积,有这样的2行,面积是6平方厘米。
练习2:
师:这几个数据中谁是每行单位面积的个数?谁又是对应的行数?
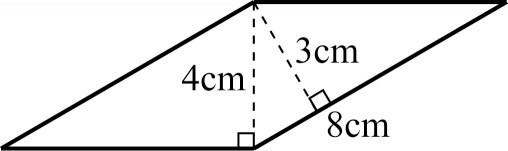
生:8是每行单位面积的个数,3是行数。
师:4对应的底在哪里?
生:下面水平的那条边。
【设计意图:通过追问底和高表示的意思,继续强化度量的本质和面积的含义。同时解决平行四边形面积计算中学生最易出错的问题,强化对应关系,深化概念的理解。】
五、经验迁移,再次猜想
师:带着研究平行四边形面积的经验,再看看这几个图形(三角形、梯形、圆),它们能用这种方法解决吗?
生:梯形可以,可以将它竖着剪开,然后将一部分翻转拼成长方形。
生:三角形也可以,把它从中间裁开,平移后翻转变成正方形。
师:先不论这样裁剪能否拼成长方形和正方形,同学们刚才觉得不能用这种方法求面积,而现在觉得可以了,对吗?
生(齐):对!
师:两位同学运用的是这两种方法(不整齐→整齐;新知→旧知)中的哪一种?
生:第二种。
师:长方形、正方形是我们学过的旧知,从今天开始,平行四边形属于新知还是旧知呢?
生:新的、旧的……(最后齐声)旧知!
师:对!今后求未知图形的面积时,我们不仅可以将它们转化为长方形、正方形,还可以转化为平行四边形后用每行单位面积的个数乘行数来求。
师:圆形能用这种方法求面积吗?
生:不能,因为它没有边,也没有角。
师:回忆研究平行四边形面积的过程,刚开始同学们觉得它没有直角不能用这种方法,后来将它转化成了有直角的图形,就能用这种方法求面积了。圆没有直边,你能想办法让它有直边吗?
生:在圆的正中间画一条线。
师:我画了两条(下左图),观察其中一部分,它像什么?
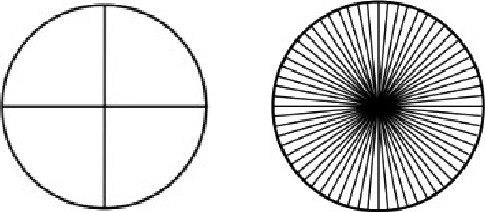
生:像四个三角形,但是有一条边是弯的。
师:如果再多一些直边呢?
生:还是有点弯。
师:再增加直边呢?(课件演示穿过圆心的直径越来越多,如上右图)
生:越来越像三角形了!
师:如果你已经掌握了三角形面积的计算方法,那么你会求圆的面积吗?
生:可以!
师:今天的作业就是选择其中一个图形(圆形、三角形、梯形),探索怎样将它转化成“旧”的图形,用“每行单位面积的个数×行数”的方法求出它的面积。
【设计意图:最后的拓展延伸是对转化思想的再次应用,让学生体会到所有平面图形的面积都可以用“每行单位面积的个数×行数”的方法得到,渗透求面积的一般方法。圆的分割带来的以直代曲和极限思想,培养了学生的想象能力。】
顶一下
(0)
0%
踩一下
(0)
0%
上一篇:“实际问题与方程”教学设计
下一篇:评刘延革老师“图形的面积”一课
- 发表评论
-
- 最新评论 进入详细评论页>>