“假分数假分数”的认知及其教学研究
——兼评罗鸣亮老师“真分数和假分数”教学 

 

    一、难在何处：假分数的认知分析

 

    长期以来，假分数的认知是分数概念教学中公认的一个难点。究竟难在何处？

    课前调研访谈表明，从没接触过假分数的学生第一次看到5/4，当教师要求作出解释时， 会感到非常诧异：一个月饼，平均分成4份，怎么会取出5份呢？有的学生甚至认为这不是一个分数。 

    究其原因，有教师认为：“原因之一，是教材关于分数意义的概括给学生认知造成了障碍。”“原因之二，是学生原有认知的负迁移。”意指“学生的前认知中，都习惯于把所看到的两个圆看作单位‘1’”。

    两个原因是否都确切？分析如下。

 

    1.分数初步认识的局限性 

    对于“原因之一”，有必要指出，教材关于分数意义的描述性概括“一个物体、一些物体等都可以看作一个整体。把这个整体平均分成若干份，这样的一份或几份都可以用分数来表示”能涵盖假分数吗？

    举例来说，把一个整体平均分成 4份，这样的4份、5份用分数来表示就是4/4、 5/4。 可见，教材的概括包括了假分数。 考虑到“一个整体”容易使学生产生误解，有教师建议先说明单位“1”，再概括分数的意义 一个物体、一些物体等都可以看作一个整体。一个整体可以用自然数1来表示，我们通常把它叫做单位“1”。把单位“1”平均分成若干份，这样的一份或几份都可以用分数来表示。 

    如此描述，用“单位‘1’”替换“整体”，似乎好一些。能解决问题吗？未必！

    因为真正的原因在于学生的理解局限于整体与部分的关系，认为部分不能大于整体。而学生之所以这样理解分数，背后的原因在于学习假分数之前，我们不断地在强化“整体与部分的关系”，而且教学中所出现的分数，几乎全是分子小于分母。

    笔者清晰地记得，20世纪80年代初，全国统编教材按照1978年的“小学数学教学大纲”将分数的教学划分为两个阶段，当时不少老教师会提醒三年级的教师：教学分数的初步认识，不宜过分强调整体与部分的关系。如今，这样的提醒早已听不到、看不到了。 

 

    2.单位“1”内涵的发展性 

    同样，原因之二也有前因后果。三年级教学分数的初步认识时，我们所采用的图示或所举的实际事例，通常都是把一个图形或一个物体看作整体（单位 “1”）。

    到五年级再次教学分数的意义，大家都会强调：几个图形、一些物体等也都可以看作一个单位 “1”。

    而到学习假分数时，我们又要学生把一个图形或一个物体看作单位“1”。

    即单位“1”（整体）的认知过程如下： 

 

 

    由此，学生出现一时的不适应，本是情理之中、意料之中。其实，两个原因归结为一点，就是分数认识教学的阶段性。

    从理解分子小于分母的分数到理解分子等于、大于分母的分数，是分 概念教学总归要经历的一个关节点，也是学生学习分数必须跨过的坎。

    充分认识教学的阶段性，以及学生认知关节点的合理性、必然性，有助于教师调整、平和心态，增强放手让学生自己质疑问难的信心与胆识。

 

    3.学生的真实困惑 

    罗鸣亮老师的课前调研告诉我们，学生的真实困惑，除了单位“1”的识别与表征，还有他们自己的问题：“假分数假在哪里？”这一看似“幼稚”实质反映儿童本真的问题，需要回答吗？ 

    在一次教学观摩活动上，一位学生一再地向教师提问“为什么4/4是假分数”，直到下课还一直坚持自己的看法：4/4没有超出一个整体，应该是真分数， 5/4才是假分数。 

    有教师认为“从来没有在教材和课堂上见过这样的讨论，我觉得教材中回避了这个题”，并就此请教张奠宙教授。张先生的回答非常精彩：“我觉得，这节课是谈真分数和假分数，一开始从真命题和假命题入手未尝不可。讨论的重点是区分两种‘真假’：第一种，假警察一定不是警察，假人民币一定不是人民币， 等等；第二种，假命题还是命题，假话还是一句话，等等。”“真分数和假分数是西方学者在历史上形成的。中国古代没有真分数和假分数 的区分。这种历史上给某对象命名的历史事实，没有必要让学生去发现，直接阅读教材就好了。”

    确实，假分数“假在哪里”？教材、教参都没作解释，数学史研究也难觅对其出处的考证，不像有理数与无理数、实数与虚数，顾名思义就能揣测其历史渊源，也能在数学史中找到典故、佐证。

    因此，也难怪绝大多数教师回避分数“真假”的讨论。然而，我们又不得不承认，这一令教师为难，却又萦绕学生心头不能放下的问题，连同与之相关的“假分数有什么用”，都是数学教学应该直面以对的“真”问题。

 

    二、突破难点：多样化的教学实践 

 

    1.以往的教学实践
    为了帮助学生自己跨过“分子小于分母→ 分子等于、大于分母”这个坎，以往的教学大多是精心设计一些“脚手架”，让学生拾级而上。

     例如，借助几何直观：

 

 

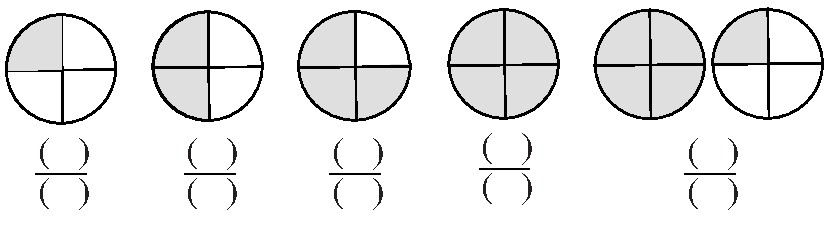
    又如，利用数轴：

 

 

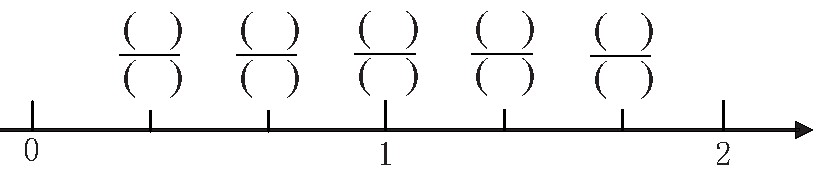
    与其他图示方式相比，数轴的优势在于能够较为直观地渗透数的连续性与可分割性。 

    两种方式的共同点都是数形结合，让学生运用最原始的数数技能，通过相同分数单位的依次计数来引出假分数。为了降低难度，有的教师干脆写出分母，只让学生填写分子。 

    再如，联系同分母分数加法：

 

 

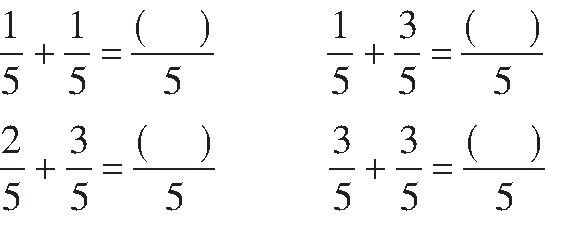
    显然，相同分数单位的累加与依次计数异曲同工，实质相通。 

    以上三种设计的实施，基本上都是先让学生独立思考，完成填空，再通过小组或全班交流来解释分数的含义，进而引出真、假分数的概念。 

    针对学生关于分数“真假”命名的疑惑，也有一些有效的教学设计。

    例如，利用分数与除法的关系：把（ ）个饼平均分给4个人，每人分到几个？ 

    引导学生从1个饼、 2个饼开始，一直继续，到8个饼、 9个饼。

 

 

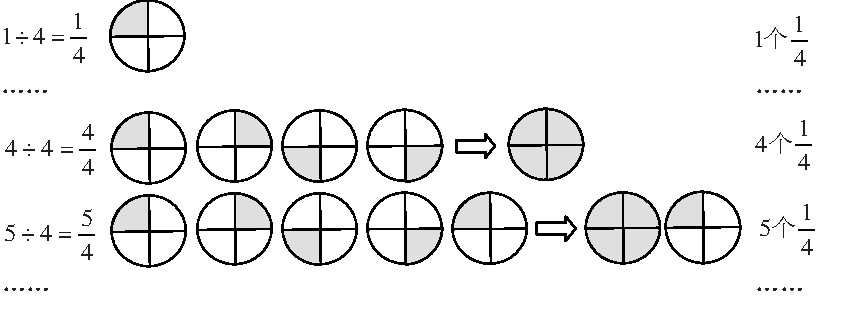
    也可以直接根据分数的意义，给出更简捷的设计：

    三个小朋友，每人分到1个饼，每个饼平均分成4份。

 

 

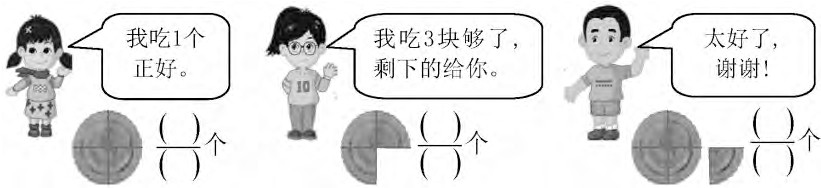
    填一填，说一说，三个小朋友分别吃了几分之几个饼？ 

    实践表明，贴近儿童生活的情境，使分数的“真假”有了生动的诠释，进而很自然地抽象出“数”，生成合情合理的解释：4/4其实是整数1，5/4是1和1/4合成的数，所以它们不是真分数。 

    事实上，也只有沟通假分数与整数、带分数的联系，才能真正理解何为“假的”分数。 

 

    2.罗鸣亮老师的教学演绎 

    罗老师的教学，兼具以上设计的优点，又别具一格。 

 

    （1）教与学进入学生的最近发展区 

    在一次大型观摩活动中，一位名师开门见山，板书课题。不料，学生纷纷插话“学过了”。

    为了不让听课教师失望，这位名师急中生智，要求学生回答问题时，回忆没学时的想法再来说。如此教学，倒也有板有眼，毕竟名师的精心预设自有不少可圈可点之处。

    这虽是舞台上表演型教学的“绝招”，但与平时教学中，不问学生是否已知，也不管他们知道了多少，一概将学生视为一张白纸，按“零起点”实施教学的常见现象，可谓“如出一辙”。

 

    如何将“新授”定位在学生的真实起点上？如何让起点参差不齐的学生各得其所？罗老师的处理令观摩者眼前一亮。

    基于课前调研，多数学生知道了真分数、假分数的定义，且能准确识别。所以，他采用“学生教学生”的策略，让知道的学生举例说明讲给不知道的学生听。然后及时调整，将教学导入学生学习的最近发展区。于是，“不让一个学生掉队” 与“不让一个学生陪读”这两个近乎苛刻的要求，实现了和谐统一。

 

    （2）“四能”培养成为教学的主线 

    学习的深入，始于“激将法”。罗老师诱导学生说出自己的疑问、困惑，使“四能”的培养目标落实在基础知识教学过程中。 

    发现问题、提出问题，一直是我国数学教育的短板，现有的研究主要集中于创设问题情境，启发学生根据已知的条件提出问题，并分析、解答。

    这固然是一种有效的训练形式，但笔者始终认为，更重要的、基本的路径在于平时教学中学生的质疑问难。

    罗老师的教学为我们提供了一个值得借鉴的范例。

    在这节课中，由学生自己发现问题、提出问题，通过一系列的学习活动最后 解决这些问题，成了贯穿课堂教学潜在的主线。 

 

    （3）让探究随机生成 

    这是本课最突出的一个亮点。 

    上面介绍的众多教学设计，都是教师研制学习材料，教师指示学习方式。虽然也有学生的独立思考、交流对话，但终归是教师说了算，学生在预设的轨道上走。而罗老师的教学，彻底放权，让学生自己选择“研究方法”。

    于是，无论是假分数的个性化表征，单位“1”的争论辨析，还是真、假分数与数轴上点的对应练习，以及真、假分数的现实原型的构造，所有这些富有探究性的活动自然而然、顺理成章地成为学生借助数形结合探究释疑的自主学习过程。 

    根据建构主义的观点,学生的前概念不可能通过知识传授的方式由科学概念代替，而必须由学生自己通过经验与知识的转化，实现由前科学概念或错误概念向科学概念的转变。 

    如此放手的生成性教学，全凭教师的教学机智、教学智慧，需要因势利导、随机应变的功力，非一般教师都能轻松驾驭。

    因此，给出上述教学设计，旨在提供经过实践检验的、“可复制”的教学样例。 

 

    （4）从“讲道理”走向深度学习
    罗鸣亮老师颇具鲜明特色的教学主张是“做讲道理的数学老师”。在这节课中，学生成了讲道理的主体，他们在群体争辩、师生互动中生成了理解，达成了共识。 

    罗老师自拟的课例研究主题“源于学生真 问题的深度学习”恰如其分地概括了本课的又一特色。 

    近几年来，深度学习已成为人工智能领域、基础教育领域的高频词。

    一线教师最想弄明白的问题是：深度学习“深”在哪里？

    对此，有教育学研究者回答“：

    首先‘深’在人的心灵里，‘深’在人的精神境界上。还‘深’在系统结构中，‘深’在教学规律中。” 

    这样的理论回答，能够在教学理念层面上给教师一些启迪，但在实践层面上，具体到一节课，深度学习究竟“深”在何处，仍然是执教者必须基于本学科特点、学生学情与教学经验，发挥实践性智慧才能破解的问题。 

    罗老师的教学案例，开宗明义确立了本课源于学生真问题的深度学习着力点：把什么看作单位“1”，假分数假在哪里，假分数有什么用。

    本课的教学叙事，又让我们进一步看到，学生是怎样在教师不露痕迹的点拨之下，运用自行选择的数形结合方法，通过探究与讲道理，从“知其然”走向“知其所以然”。

    在这个过程中，学生学习动机的高度激活、高度投入，活动经验的充分积累与知识意义的个性化建构，都表明这是“学生围绕具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的有意义的学习过程”。深度学习名副其实。

 

    三、完善建议：补充两量比较的实例

 

    在数学中，分数的定义是：形如a/b的数集，其中，a、b都是整数，且b≠0。据此可以认为，分数的本质是两个量的相对关系。所以，分数除了表示整体量与它的部分量之间的关系，还可以表示两个相对独立量之间的关系。例如：

    男生人数占总人数的3/8，表示整体与部分的关系； 

    男生人数相当于女生人数的3/5，表示两个相对独立量的关系。 

    后者也同时揭示了两类关系之间的某种联系。 

    也正因为如此，在用线段图表示分数、百分数实际问题的数量关系时，我们都会注意用一条线段表示整体与部分的关系，用两条线段表示两个相对独立量的关系。 

    由此，教学假分数时，不宜清一色全是整体与部分关系的例子与图示，应该酌情补充两个相对独立量之间关系的例子。例如：

 

 

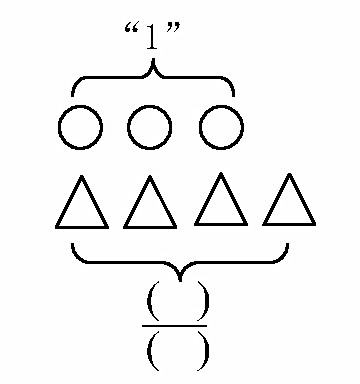
    当然，认识不能一次完成。用假分数表示相对独立量之间的关系，完全可以在后继课时中作为练习出现。 

    为了帮助学生突破感知与思维的定势，在分数初步认识教学的后期，就可以出现类似的填空练习。

    事实上，三年级的一般学生就能自行看图理解。例如，笔者曾抽取4个在分数的初步认识教学中从未出现两个相对独立量关系的班级，在单元学习结束时进行如下测试（教师不作任何提示）。 看图填空：

 

 

    小亚吃的是小胖的( ) /( ) 

 

 

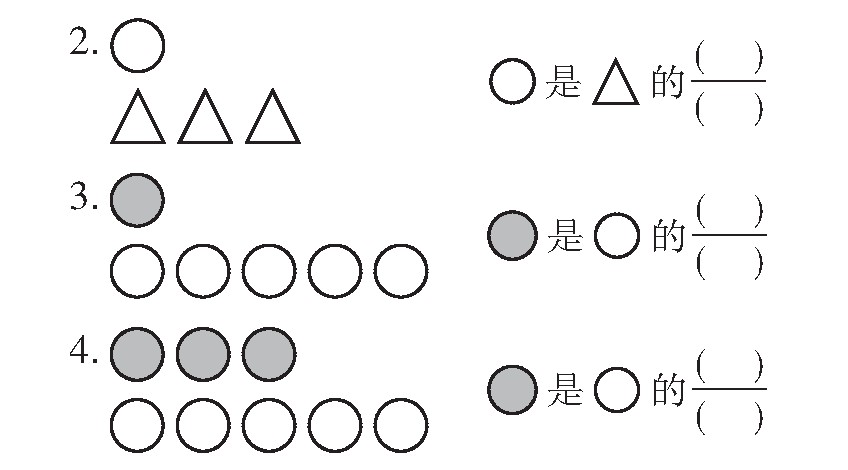
    结果如下表：

 

 

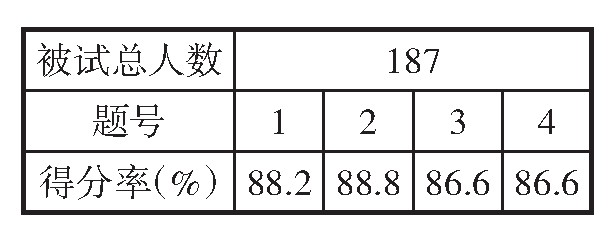
    数据显示，超过86%的三年级学生能够无师自通。有了这样的铺垫，五年级教学真分数和假分数，自然会更加顺利。