平行四边形和梯形单元练习

一、在变与不变中实施动态想象
师:(课件出示图1)你看到了什么?
师:把这4个点连起来,想象一下会是什么图形。
生:平行四边形。
师:大家都认为是平行四边形吗?(显示背景方格,如图2)
生:是四边形。
师:怎么回事?
生:因为只有一组对边互相平行。
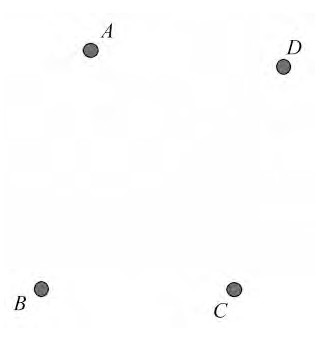
图1

图2
师:请你想象,怎样才能变成平行四边形?
生:把点D往上移。
师:随便移吗?
生:只能移一点点,和A在同一条水平线上。
课件动态演示,移动点D,联结AD和BC,如图3。
师:怎样的四边形是平行四边形?(两组对边分别平行的四边形)
师:继续想象,点D往左移可能出现什么图形?
生:直角梯形。(课件出示图4)
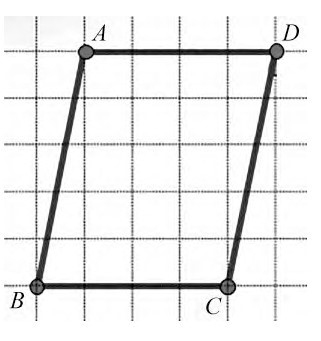
图3
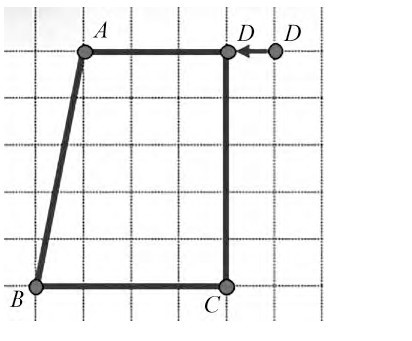

图4
师:为什么是梯形?(因为是只有一组对边平行的四边形)
师:怎样的梯形是直角梯形?(有一个角是直角的梯形)
师:我们继续向左移动点D,(课件出示图5)现在把点A、B、C、D顺次联结起来,会是一个什么图形?
生:等腰梯形。
师:怎样的梯形是等腰梯形?(两腰相等的梯形)
师:继续向左移动点D,想象一下,可以得到哪些图形呢?(课件出示图6)
生:可以得到三角形、直角梯形、梯形、平行四边形。
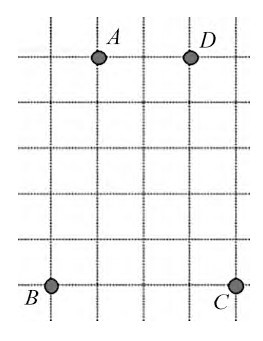
图5
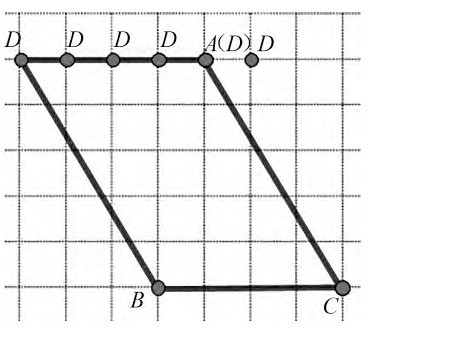
图6
师:点D一直在移动,除三角形外,怎么都是梯形或平行四边形?
生:因为点D在移动的时候总是保持了一组对边平行,当另一组对边不平行时是梯形,平行时是平行四边形。
师:继续想象,如果点D继续往左移动,会变成什么图形?(生答略)
师:点D在向左移动的过程中,分别会出现平行四边形、三角形和梯形,在这些变化之中,什么始终不变?
生:高不变。
师:不变的高在哪里?(AD和BC间的距离)
二、在动手操作前实施动态想象
课件出示:在平行四边形中添上一条线段,把它分割成两个完全相同的图形。
师:请先想象一下,你会怎么画线段,会分成什么图形,想好以后在练习纸上画一画。
展示学生作品(图7):
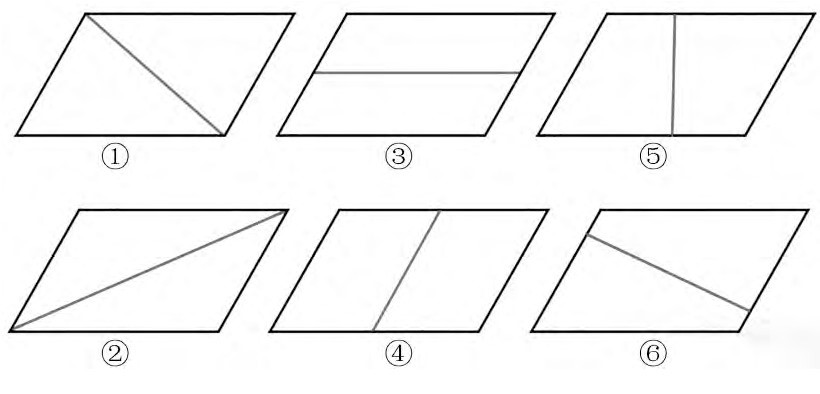
图7
师:看到这些分割的结果,你有什么发现?
生:我发现,1个平行四边形可以分成2个完全相同的三角形、平行四边形或梯形。
生:也可以说2个完全相同的三角形、平行四边形或梯形可以拼成一个平行四边形。
师:既然两个完全相同的图形可以拼成一个平行四边形,那么其中一块的大小与平行四边形有什么关系?
生:其中一块的大小是平行四边形的一半。
师:想一想,是不是随便画一条线段,一定能分出两个完全相同的图形?
生:画平行四边形的两条对角线,找到中心点,过中心点任意画一条直线,就可以把一个平行四边形分成两个完全相同的图形。
展示学生作(图8):
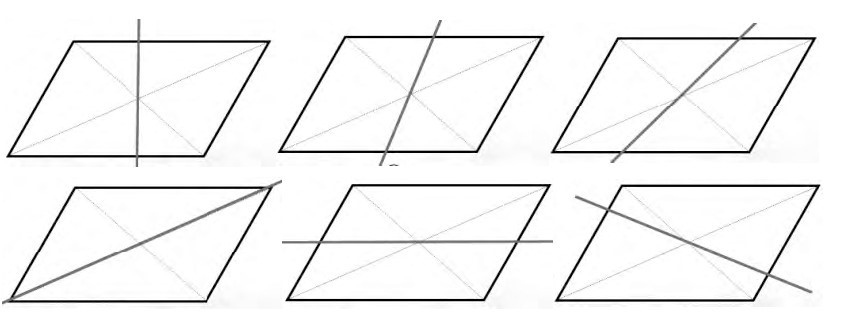
图8
三、在思辨中实施动态想象
课件出示:在两个相同的直角梯形中各添加一条线段,想一想,分成的平行四边形和正方形谁更大呢?如(图9,其中AD=AB=1/2BC)
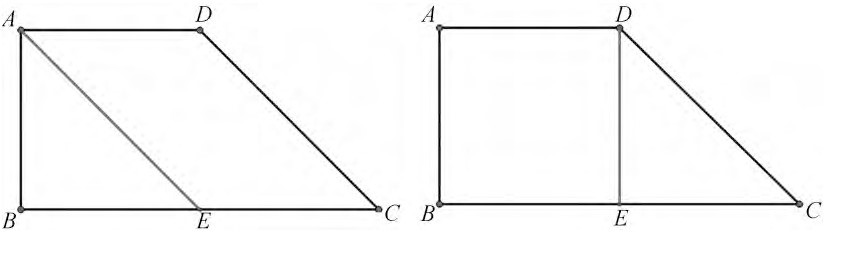
图9
生:一样大。
师:两个图形完全不一样,为什么大小一样呢?
生:可以在左图中联结DE,在右图中联结AE,并分别编号(图10),会发现 (1)(2)(3)(4)号是一样大的,所以两个图形分别去掉 (1)号和(4)号,剩下的平行四边形和正方形一样大。
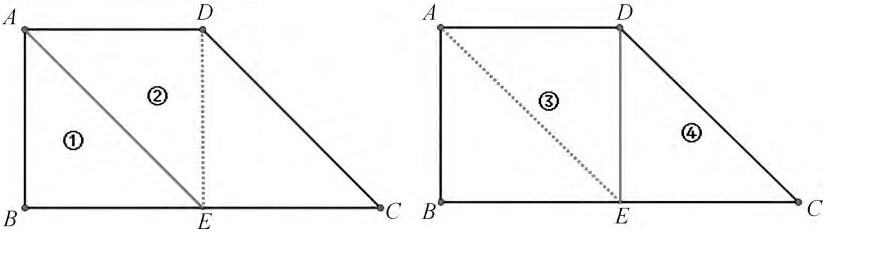
图10
生:这两个直角梯形都可以分成3个相同的直角三角形,平行四边形和正方形都是由两个直角三角形组成的,它们的大小是一样的。
师:把它们放在格子图中更容易看明白。(图11)

图11
师:(指图9)左图中的平行四边形能再大些吗?右图中的正方形能再大些吗?它们还能再小吗?怎么变小?(生答略)
师小结:通过分一分,大家又有很多新的发现,这些发现对我们以后的学习会很有帮助。
四、在合作交流时实施动态想象
师:刚才我们学习了这么多,主要从什么角度进行的?(板书:边)四边形除了有4条边,还有4个角。(板书:角)
师:想一想,正方形和平行四边形的内角和是几度?(板书:内角和)
师:由内角你们会想到什么?接下来我们一起来研究四边形的外角和。
师:通常我们把每条边的延长线与邻边组成的角看作外角。(课件演示长方形的外角)你们看到几个外角?(略)
出示要求:先独立思考,然后四人小组交流,最后在练习纸上解答。
1. 正方形的外角和是多少度?你是怎样思考的?
2. 图(1)和图(2) 都没有具体的度数,请你先想象,再思考它们的外角和是多少度。
3. 你们组有什么发现?
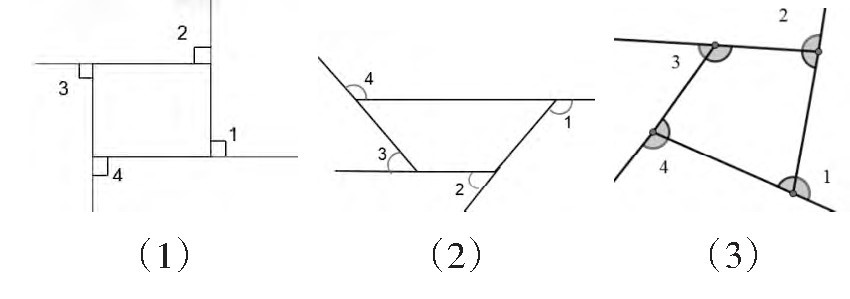
图12
教师组织全班反馈。
生:正方形的外角和是90°×4=360°。
生:图(2)梯形的每一个内角与相应的外角加起来正好是一个平角,这样的4组减去内角和360°就是外角和了,180°×4-360°=360°。
生:图(3)与图(2)外角和的算法一样,也是360°。
师:对于四边形的外角和,你有什么猜想?
生:四边形的外角和是360°。
师:请试着想象,假如你有一种神奇的魔力,可以把每个四边形都收缩成一个点,猜猜结果会怎样?
生:是一个周角,就是360°。
师:真是这样吗?如果用这样的方法继续研究五边形、六边形、七边形等的外角和,会出现怎样的结果呢?有兴趣的同学课后可以继续研究。
顶一下
(1)
100%
踩一下
(0)
0%
- 发表评论
-
- 最新评论 进入详细评论页>>