“圆柱的体积”教学设计
湖南省常德市西湖区裕民小学 卿锡吾
教学目标:
1.使学生掌握圆柱体积公式,会用公式计算圆柱体积,能解决一些实际问题。
2.让学生经历观察、操作、讨论等数学活动过程,理解圆柱体积公式的推导过程,引导学生探讨问题,体验转化和极限的思想。
3.在图形的变换中,培养学生的迁移能力、逻辑思维能力,并进一步发展其空间观念,领悟学习数学的方法,激发学生兴趣,渗透事物是普遍联系的唯物辨证思想。
教学重点、难点:
1.圆柱体积计算公式的推导过程并能正确应用。
2.借助教具演示,弄清圆柱与长方体的关系。
教学过程:
一、复习导入
1.圆面积公式是怎样推导的?
2.怎样求圆柱的侧面积、表面积?计算公式各是什么?
3.怎样求长方体、正方体的体积?计算公式是什么?
二、经历体验,探究新知
1.思考下列问题。
(1)图1中甲圆柱与乙圆柱谁的体积大?它们的什么条件相同?
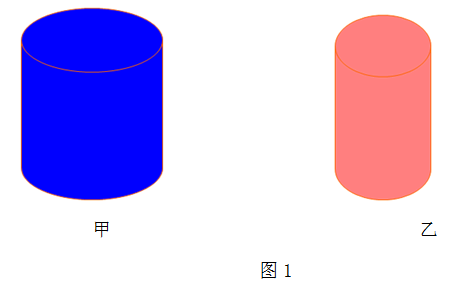
(2)图2中上、下叠放的两个圆柱的体积哪个大?它们的什么条件相同?
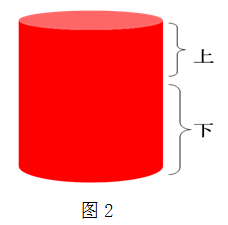
(3)圆柱体积的大小与哪些条件有关?
2.小组合作,探究新知。
(1)启发猜想:我们要解决圆柱的体积的问题,可以怎么办?(引导学生说出圆柱可能转化成我们学过的长方体。并通过讨论得出:反圆柱的底面积分成许多相等的扇形,然后反圆柱切开,再拼起来,就转化近似的长方体了。)
(2)学生以小组为单位操作体验。
把圆柱的底面积分成许多相等的扇形,然后把圆柱切开,再把它拼起来,就转化成近似的长方体了。使学生进一步明确分的份数越多,圆柱体就越接近长方体。同时演示一组动画(将圆柱底面等分成32份、64等份、128等份……)
(3)学生小组汇报交流。
近似的长方体的体积等于圆柱的体积,近似的长方体的底面积等于圆柱的底面积,近似的长方体的高就是圆柱的高。根据长方体的体积等于底面积乘高,得出圆柱的体积也等于底面积乘高。
教师根据学生汇报,用教具进行演示。
(4)概括板书:根据圆柱与近似长方体的关系,推导公式。
三、实践应用,巩固新知
1.火眼金睛判对错。
(1)圆柱的体积=底面周长×高。( )
(2)底面积和高分别相等的两个圆柱体积相等。( )
(3)圆柱的体积公式是由长方体的体积公式推导而来。( )
(4)圆柱的底面积不变,高扩大3倍,那么体积扩大9倍。( )
(5)长方体、正方体和圆柱的底面积和高都相等,那么它们的体积也一定相等。( )
2.计算下面各圆柱的体积。
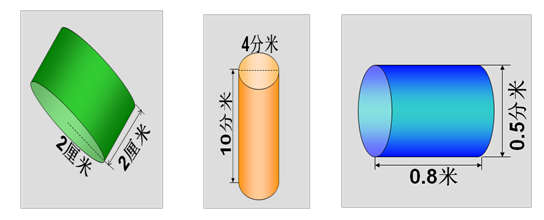
3.实践练习。
(1)把一个棱长12分米的正方体木块切削成一个体积最大的圆柱
体,这个圆柱的体积是多少立方分米?
(2)将一个棱长为12分米的正方体钢材熔铸成底面半径为3分米的圆柱体,这个圆柱有多长?
4.讨论、展示。
(1)已知圆的半径和高,怎样求圆柱的体积?
(2)已知圆的直径和高,怎样求圆柱的体积?
(3)已知圆的周长和高,怎样求圆柱的体积?
四、反思回顾:通过本节课的学习,你有什么收获吗?
五、板书设计:
圆柱的体积
根据圆柱与近似长方体的关系,推导公式:

●温馨提示:您想阅读该内容的教学视频,请链接——
●温馨提示:您想下载该内容的教学课件,请链接——
●温馨提示:您想阅读该内容的教学反思,请链接——
●温馨提示:您想下载该内容的教学课件,请链接——
●温馨提示:您想阅读该内容的教学反思,请链接——
顶一下
(0)
0%
踩一下
(0)
0%
下一篇:“圆锥的认识”教学设计
- 发表评论
-
- 最新评论 进入详细评论页>>