未来已来，不管您愿不愿意，我们都将迎来一个智能时代。技术正在改变我们的生活，也必将改变我们的数学教育。

    近日，笔者与新世纪小学数学教材编委会、新思维小学数学教材编委会以及“魔法园丁”技术团队合作，作了一次基于AR(Augmented Reality，增强现实)技术进行小学数学教学的尝试。这是课堂改进的-小步，但希望是AR进入数学课堂的一大步。

    计算机科学与教育技术领域的研究人员给予AR的定义多种多样。比较普遍认同的观点是：它是一种将真实世界信息和虚拟世界信息“无缝”集成的新技术，是把原本在现实世界一定时间空间范围内很难体验到的实体信息（视觉、听觉、味觉、触觉等），通过电脑等科学技术，模拟仿真后再叠加，将虚拟的信息应用到真实世界，即真实的环境和虛拟的物体实时地叠加到了同一个画面或空间，被人类感官所感知，从而达到超越现实的感官体验。

    AR系统具有三个突出的特点:真实世界和虚拟的信息集成；实时交互性；在三维尺度空间中增添定位虚拟物体。

    这次尝试的内容是六年级下学期“圆柱和圆锥体积”的练习课，属于偏向数学能力发展的拓展课程，取名“让画出的图形转起来”。拟定的教学目标是：经历自主操作的过程，感受平面旋转与立体图形之间的关系，增强二维和三维之间的关系理解；能准确感知长方形、三角形旋转后形成的立体图形；经历度量、计算和推理的过程，发现同一个图形绕不同的边旋转，形成立体图形的体积不一定相同，从而进一步发展空间观念和想象能力；在解决富有挑战性的问题中，经历“变与不变”的比较过程，进一步探索变化规律，发展提高批判性思维；经历数学联系生活的过程，提升数学应用意识，体会数学学习的乐趣。

 

    一、借助微课，激活经验

 

    通过播放短视频，沟通点、线、面、体之间的关系，激活已有经验，更加直观地回忆：点动成线、线动成面、面动成体。

 

 

    教师结合当地的现实场景鸣沙山月牙泉，激活学生的经验，启发学生结合现实原型进行类比，一粒粒沙就像一个个点，铺成地就是一个面，面与面的交界山峦就是一条线，堆成一座山就是一个体。学生真切地感受到点、线、面、体就在我们身边。

 

    二、长方形的旋转

 

    1.布置任务：请在方格纸（每一小格的边长为1）上任意画一个长方形，思考沿着长边和短边旋转一周，形成的图形体积一样吗？为什么？

 

 

    2.教学时，学生画好自己喜欢的长方形后，先组织学生凭直觉猜测旋转后图形的体积结果：A.一样大；B.沿着长边旋转的体积大；C沿着短边旋转的体积大；D.无法判断。

    3.教师暂不作评论，让学生进行计算，看到底结果怎样。（计算结果保留π）

    4.学生反馈。

    生：我画的长方形的长是5，宽是3（图1），沿着长边旋转：V＝π×3×3×5＝45π；沿着短边旋转：V＝π×5×5×3＝75π，75π>45π。所以，沿着短边旋转形成的图形体积大。

    教师应用AR技术支持反馈。现场直接扫描学生所画的图形，图形便显示在电脑屏幕上（图3），点击旋转按钮，使长方形沿着长边旋转一周，屏幕上出现一个圆柱（图4），圆柱的底面半径是3，高是5。

 

 

    采用同样的方法，直观演示沿着短边旋转一周形成的图形，也是一个圆柱（图5），圆柱的底面半径是5，高是3。

    通过计算比较，结合对两个立体图形的观察，得出结论：沿着短边旋转形成的立体图形的体积大。

    5.选择例子，再次进行判断比对。

    为了丰富例子的多样性，选择一个长和宽相差比较大的长方形作品（图2），长是12，宽是2。计算结果与AR技术再一次印证，沿着短边旋转形成的立体图形的体积大（图6、图7）。

 

 

    师：是不是所有的长方形都是沿着短边旋转形成的图形体积大？有谁能找出反例吗？或者谁能说明其中的道理？

    进面引导学生进行一般化的分析：假设长方形的长是a，宽是b，那么沿着长边旋转形成的图形体积是π×b×b×a：沿着短边旋转形成的图形体积是π×a×a×b。因为a>b，所以π×a×a×b>π×b×b×a，即沿着短边旋转形成的图形体积大。

    师追问：会不会有体积相等的时候？

    生：当长方形的长和宽相等时，即当这是个特殊的长方形（正方形）时，两种旋转方式形成的图形体积相同。

 

    三、半个长方形的旋转

 

    1.布置任务：有一个长方形（下图），长是8厘米，宽是6厘米，沿着米字格虚线中的一条把长方形分成大小形状相同的两部分，涂上不同的颜色，并分别标注A、B沿着长方形短边旋转一周，A、B两部分旋转而成的图形体积样吗？

 

 

    2.师：把长方形分成大小形状相同的两部分，有哪几种分法？先让学生分一分，涂一涂。根据给定的虚线，课堂上学生大致有以下四种分法：

 

 

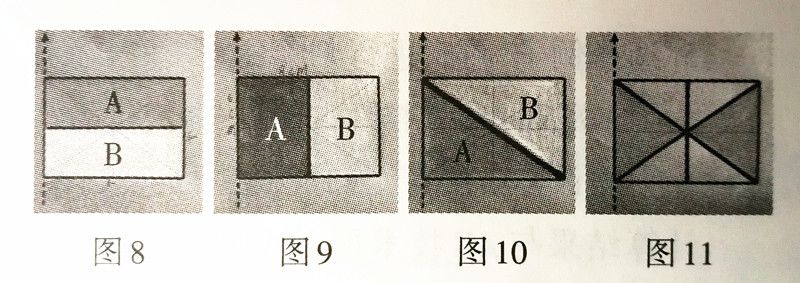
    虽然图11中涂色部分的面积是长方形的一半，但两部分形状不同，不是用一条线分开，因此不符合要求。因为要求沿着给定的虚线分割，所以主要分法是前面3种。（从后续学习来说，也可以放开让学生探讨各种可能的分法，即只要经过中心点的直线都可以，但本课教学中不展开探讨）

    3.师：A、B两部分旋转而成的分别是什么图形？体积一样吗？为什么？

    （1）在讨论前，鼓励学生凭直觉大胆猜。学生有3种猜测：A.一样大；B.不一样大；C.无法判断。

    在讨论的过程中，总是让学生先思考，不断地在脑中进行操作，强化表象，锻炼想象能力。

    （2）讨论第一种分法。

    A、B两部分旋转而成的图形都是圆柱（图12），且圆柱底面的面积相等，高相等，因而圆柱的体积也相等。结果是：V＝π×8×8×3＝192π（立方厘米)。

 

 

    （3）讨论第二种分法。

    A部分旋转而成的图形是一个圆柱，圆柱的底面半径是4厘米，高是6厘米，圆柱的体积是：V＝π×4×4×6＝96π（立方厘米）。

    对于B部分旋转出来的图形，学生根据生活经验说是一个“空洞”。教师追问“空洞”的体积是多少，并引导学生进行如下计算：

    A、B两部分旋转而成的圆柱(图13)的体积是：V＝π×8×8×6＝384π（立方厘米），已知VA＝96π立方厘米，那么VB＝384π―96π＝288π（立方里米）。288π>96π，所以B部分旋转出来的图形体积大。

 

 

    基于AR技术的直观演示，经过分离可清渐地观察到，B部分旋转而成的立体图形是大圆柱减去小圆柱后的剩余部分(图14)。

    （4）讨论第三种分法。

    A部分旋转而成的图形是一个圆锥，底面半径是8厘米，高是6厘米，圆锥的体积是：VA＝1/3×π×8×8×6＝128π（立方厘米）。

    B部分旋转出来的图形是什么呢？先让学生想象，再用AR技术演示验证。（两部分分离前后的图形分别为图15图16）

 

 

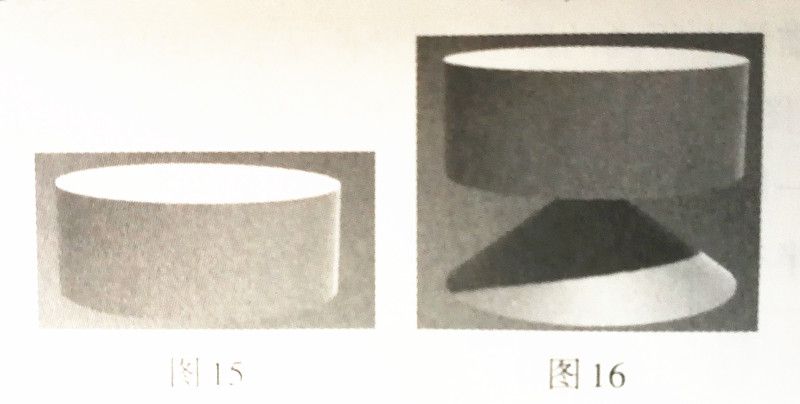
    大部分学生一开始会直观地认为B部分旋转出来的图形和A部分是一样的，都是圆锥。教师引导学生展开想象，B部分旋转出来的图形既非圆锥，也非圆柱，而是圆柱减去圆锥的剩余部分。

    有学生认为：B部分旋转而成的图形体积是A、B两部分旋转出的圆柱体积减去A部分旋转出的圆锥体积，结果是：VB＝384π―128π＝256π（立方里米）；

    也有学生认为：B部分旋转而成的图形体积是A部分的2倍，这是因为A部分旋转出的圆锥体积是圆柱体积的1/3，所以剩下的就是圆柱体积的2/3。

    （5）引导学生小结提炼：将一个长方形分成大小和形状都相同的两部分，旋转后形成的立体图形的体积不一定相同。

    学生习惯将平面图形面积的比较结果类比到旋转形成的立体图形体积比较的结果，类比后的结果越是不一致，越容易激发学生的批判性思维。

 

    四、三角形的旋转

 

    1.布置任务：有一个三边长分别为10cm、8cm、6cm的直角三角形，沿着其中一条边所在的直线分别旋转一周，形成的三个立体图形的体积一样吗？如果不一样，猜测一下哪一个体积最大,并请说明理由。

    2.学生猜测,尝试解答。

    绝大部分学生认为不一样。师追问：哪个最大呢？

    据课堂统计，认为沿着6厘米的边旋转体积最大的学生有15位，认为沿着8厘米的边旋转体积最大的有6位，认为沿着10厘米的边旋转体积最大的有22位。

    3.四人小组分工合作,分别沿着三角形的三条边进行旋转操作，讨论哪一种情况下体积最大。

    4.组织学生进行精确计算。

    （1）沿着6厘米的边旋转而成的是一个圆锥：V1＝1/3×π×8×8×6＝128π（立方厘米） 

    （2）沿着8厘米的边旋转面成的是一个圆锥：V2＝1/3×π×6×6×8＝96π（立方厘米）

    （3）沿者10厘米的边旋转面成的是什么图形呢？学生讨论发现，它形似陀螺，由两个圆锥组成。圆锥的底面半径是直角三角形斜边上的高（高为6×8÷2×2÷10＝4.8厘来）。因此，立体图形的体积是：V3＝1/3×π×4.8×4.8×10＝76.8π（立方厘米）。

    （4）应用AR技术，将学生涂色后的三角形现场扫描，即时生成旋转而成的立体图形并进行直观验证。得出结论：沿着最短边旋转面成的立体图形体积最大。沿着最长边旋转而成的立体图形体积最小（图17）。

 

 

    五、其他團形的旋转 

 

    1.平面图形与立体图形配对。

    学生通过观察，想象平面图形A、B、C旋转一周能形成下面哪一个立体图形（图18）。并尝试连线。应用AR技术演示比对。 

 

 

    教师在设计匹配选项时没有一一对应。有的平面图形对应两个立体图形。如A对应①和②，C对应着③和⑤。

    2.从平面图、立体图过渡到生活中的图。

 

 

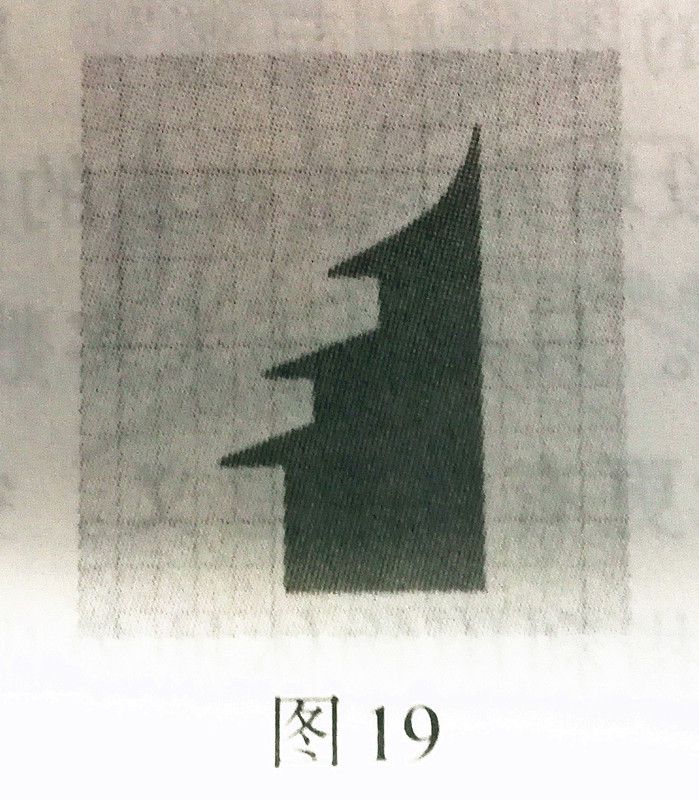
    先让学生观察平面图（图19）。想象旋转得到的会是生活中的什么实物。最后教师分步演示（图20、图21）。 

 

 

    3.学生创作一个不规则的平面图形。想象沿着指定的一条线旋转一周会形成一个怎样的立体图形。然后AR现场扫描。即时生成立体图形。全班欣赏（图22、图23）。

 

 

    六、课堂小结 

 

    引导学生回顾学习过程。分享感悟。

    学生进一步体会平面图形和立体图形之间的关系，分享操作的经验和想象的乐趣，体会数学的美妙之处。