小学数学如何实现从直观到抽象的飞跃
———谈教材里关于“图形的运动”的处理

    本世纪初进行的课程改革，把“图形的运动”列入小学教材，这是一个意义深远的决策。但是，各种教材的编写者在展现这一内容时，对其内在的数学本质揭示得不甚确切，表现形式也有些含混。
    我们首先要问，为什么在小学里要将平面图形的运动列入课程标准呢？ 《数学课程标准（2011）》没有明确说明。大体说来，应是为了达到以下目的：
    第一、观察和认识现实世界里物体的平移、旋转、翻折的运动现象。
    第二、建立平面图形运动的几何框架。
    第三、了解图形在刚体运动的作用下大小、形状不变的性质。
    第四、会用平面图形的平移、旋转、轴对称作简单的应用。
    下面我们围绕某些教材相关单元中存在的问题进行一些评论，并提供一些建议。

    一、实物的运动和平面图形的运动不是一回事

    在现实生活中，物体的运动大多是立体图形的运动。 例如，人在行动、车在开动、门在转动、书在翻动、电梯的升降运动、推拉门的滑动，等等。
    小学数学教材中“平移与旋转 ”的主题图，是用许多照片来显示实际物体的平移与旋转运动现象的。（如图1、图2）学生可以根据自己的生活经验，判断图片里的实物究竟是在移动还是在转动。也就是说，我们要求学生判断的是照片里的那个立体物体所做的运动，而不是照片里平面图形的运动。
    比如，教材里一张直升机的照片，我们要求学生想象直升机会移动，而且它的螺旋桨会转动，而不是说照片里的图形在转动。（照片里直升机一动也不动）

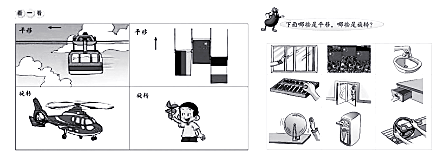
    这就是说，物体的运动现象和平面图形的运动，虽然都有“运动”二字，却并不是一回事。从观察实物的运动状态到探究“平面图形的运动”，其间的距离相当大。我们的任务是实现从直观的物体运动到抽象的平面图形运动的飞跃。
    那么，为什么在小学里不直接研究立体图形的运动，只研究平面图形的运动呢？
    这一方面是因为立体物体的运动太复杂，例如物体的旋转，就有绕直线轴的转动和绕一点的转动两类，理解起来比较困难。 因而在义务教育阶段直至高中的数学课程中，都没有正面地接触立体图形的运动。
    另一方面，由于电影、电视（不包括3D）里大量出现的都是平面图形的运动，在电视画面上看缆车的滑动、电梯的移动、窗户的移动，其实都是平面图形的移动。尤其是儿童在熟悉的动漫里看到熊猫的画面在移动，电影里孙悟空的金箍棒在转动，照片里蝴蝶的左右两半可以折叠相重，等等，都是具有现实生活原型的平面图形的运动。

    二、通过一系列的“数学活动”构建平面图形运动的平台

    教材里的主题图只是认识物体运动的开始，我们的目标是要建立平面图形运动的数学平台。按照数学“四基”教学的要求，教材中不妨设计一系列的数学活动，让学生在实际操作中逐步完成这一过渡。具体建议是：
    步骤 1.1 想象和认识生活中物体运动的现象。例如电梯和直升机。
    步骤 1.2 在课堂上进行立体物体运动的实际操作。例如，可以带一只熊猫玩具，演示实物的平移和旋转。
    步骤 2.1 观察接近平面形状的实物的运动。 如奥运会上不断上升的国旗（平移）、菜市场里台秤上的指针（旋转）。
    步骤 2.2 在教室里取材实际操作。例如，教师先在黑板上演示把一本书进行平移、旋转作为示范，然后学生将一个铅笔盒或一块三角板在课桌上沿某方向平移、绕某点旋转一个角度。通过实际操作，体验什么是“运动”。
    步骤 3.1 抽象地把书的形状（矩形）或三角板的形状（三角形）画在黑板上，用平面图形表示书或三角板的运动。
    步骤 3.2 在方格纸上，定量化地将平面图形作运动。如,将一个三角形向右移动 3 格,将一个三角形向上移动 4 格,将一个正方形绕某点旋转 90°,将一个正方形绕某点旋转 45°。
    经过这样的 6 步，从立体到平面，从物体到图形，从定性描述到定量描绘，学生就能通过自己的数学活动体验平面图形运动的意义了。

    三、一个“基本数学活动”：三角形的重合

    众所周知，平移、旋转和翻折三种运动是最基本的平面图形运动。在小学数学教材里，往往把平移、旋转放在一起，而把翻折放在“对称”一节，并称作轴对称。为了对刚体运动有一个完整的认识，并为中学里学习平面几何打基础，建议明确提出“翻折”运动，并和平移、旋转放在一起考察。
    为了进一步贯彻 “四基”教学，给学生参与“基本数学活动”的机会，建议做以下的具有几何味道的活动：如何将两个相同的三角形重合起来。
    活动主题：将两个相同的三角形通过运动使之重合。
    1.将点A移到A'。（这只需要平移 ）
    2.将线段AB 移到A'B'（AB=A'B'）。（这需要先作平移，将点A 移至 A' 处，点B相应移到B'' 处。如果B''和B' 不重合，则需要绕点A' 做一次旋转）
    3.将两个完全一样的三角形ABC和A'B'C'，通过运动使之重合。（这时，单靠平移和旋转，可以使AB与A'B' 重合，但是还可能需要沿线段 AB 做一个翻折运动才能重合）
    活动时可以用两个相同的三角板，先用胶带粘在黑板上的不同位置，然后让一些同学上来操作完成。
    这样一来，学生就自然而然地明白为什么在小学数学里要学习平移、旋转、翻折这三种平面图形的运动了。
    学生通过这样的数学活动所积累的经验，可以为初中学习“全等三角形”内容作好直观的铺垫。

    四、平面图形刚体运动的不变性质

    平面图形的平移、旋转和翻折（轴对称）是最简单的几何运动，统称为刚体运动。
    “刚体”的意思为它是用钢铁或钢板那样的硬物构成的物体，不是橡皮泥捏出来的，可以变形；也不是冰做的，会化掉。刚体运动的重要特性是通过运动之后图形的形状和大小都保持不变，既不会放大或缩小，更不会变形走样。与这一特性相关的割补法以后要不断地使用。如推导平行四边形的面积公式，就要把一个三角形搬过去，拼起来。由于面积是不变量，最后获得底乘高的结果。
    寻求“平面图形几何运动的不变量”是一种极其重要的数学方法。众所周知，运动几何学起源于1872年德国数学家 F.克莱因探究运动群下的不变量的划时代贡献。此外，寻求变化中的不变性质也是其他学科的任务之一。物理学中的能量守恒定律、动量守恒定律就是明证。
    小学数学当然不必涉及这些，我们只是为这样的数学方法隐含地播种而已。
    “变化中的不变性”的理解并不困难。在生活中也可以举出许多例子。例如，中华文明已经有五千年历史，但是使用方块字的传统没有改变；我们的年龄不断增大，但是名字没有变，与爸爸妈妈的儿女亲情关系也没有改变。
    长期以来，我国数学教学中对不变量思想重视不够。从小学阶段开始孕育，在小学教材里提一句，也许是必要的。

    五、教材中“轴对称图形”单元的一些不恰当表述

    对于轴对称图形，更要明确指出这是平面图形的运动，不是立体图形的运动。如不加以区分，就会出现“天安门是不是轴对称图形”这样的怪问题。事实上，天安门建筑物是立体的，是关于中轴面对称的立体图形，和平面图形关于某直线的轴对称不是一回事。具体说来，我们必须明确指出“立体的天安门”和“正面拍摄的天安门照片”二者之间的区别，人脸、蜻蜓、蝴蝶的对称都是如此。
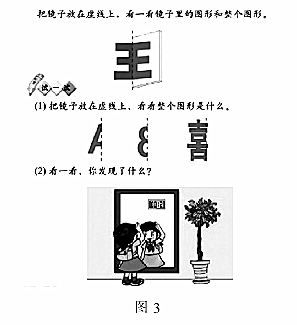
    立体图形和平面图形不加区分的做法，如果处理不当还可能出现更多的错误。 例如某教材里所谓“镜子里的图形”（如图3）其实不是轴对称图形。 因为初始的图形和镜子里的图形不在同一个平面里。 其中有一个女孩照镜子，完全是在两个不同的平面上，和轴对称相去甚远。（新教材中已删去此内容）

    六、学会“平面图形运动”的一些初步应用

    平面图形的运动，有一些重要的应用，教材中应该有所体现。
    1.用轴对称观点作艺术欣赏。
    某教材的处理是将它作为艺术欣赏，呈现数学的文化特征。（如图4）这一页的内容都取材于我国古代文物中的平面图案（只有一个“原始社会彩陶”是立体图形，应删去），突出数学的文化价值，有利于“情感、态度、价值观”教学目标的达成，值得称道。

    2.利用轴对称运动画各种图案。包括比较复杂的拼图。（如图 5）

    3.为割补法做铺垫。如前面提到的推导平行四边形的面积公式。
    4.用平移画矩形和平行四边形。根据平行定义等，一支铅笔（一条线段）平移扫过的图形是矩形或平行四边形。
    （作者系华东师范大学教授 、 博士生导师 ，《普通高中数学课程标准》研制组组长，本刊顾问）