化简比一定要用比的基本性质吗?
在人教版教材中,化简比的例题都是用比的基本性质进行计算的。在实际教学中,我发现有些题目用比的基本性质化简比较繁琐,而用求比值的计算方法或约分的方法化简相对简单。
例如,把1.5∶0.3化简成最简单的整数比。
教材的方法:
1.5∶0.3
=(1.5 × 10)∶(0.3 × 10)
=15∶3
=(15 ÷ 3)∶(3 ÷ 3)
=5∶1
用求比值的方法:
1.5∶0.3
=1.5 ÷ 0.3
=5
=5∶1
又如,把180∶120化简成最简单的整数比。
教材的方法:
180∶120
=(180 ÷ 60)∶(120 ÷ 60)
=3∶2
(这里的前项和后项同时除以180和120的最大公因数,但这个最大公因数还要先用列举法或短除法求出)
用约分的方法:
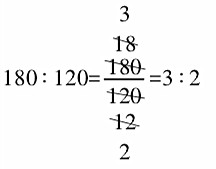
请问,化简比能不能用求比值的方法或约分的方法进行呢?(广东东莞 潘瑞莲)
化简比要求把一个比化成最简单的整数比,也就是化成前项和后项是互质数的比。
化简比大致有以下四种情况。
(1)整数比的化简:只要将比的前项和后项分别除以它们的最大公约数。
(2)含有小数的比的化简:移动小数点的位置,先把小数比化成整数比,再按整数比的化简方法进行化简。
(3)含有分数的比的化简:用两个分母的最小公倍数去乘比的前项和后项,把分数比化成整数比,再把这个整数比化简。
(4)既含有小数,又含有分数的比的化简:先把比的前项和后项都化成小数或分数,然后按小数比或分数比的化简方法化简。
一个比,常常不是只有一种化简方法,可根据相比的两个数的具体情况,灵活选用合适的、简单的方法化简。注意:不管用什么方法,化简比的依据是比的基本性质,所以教材的例题大都采用比的基本性质进行化简。
“化简比”和“求比值”是两个不同的概念,它们的目的、方法、结果,包括读法都有区别。当然,有些化简比的题目可以当作求比值做,然后写成比的形式;有些求比值的题目可以先化简比,再求比值。
——来源《小学数学教师》2016年第5期
(鲁淑琴选录)
顶一下
(0)
0%
踩一下
(0)
0%
- 发表评论
-
- 最新评论 进入详细评论页>>