小数群优秀主持人、湖南省常德市柳叶湖旅游度假区七里桥小学徐慧老师与孩子们在游戏中快乐学习！
 

    1.和差问题

    已知两数的和与差，求这两个数。

   【口诀】
    和加上差，越加越大；除以2，便是大的；和减去差，越减越小；除以2，便是小的。

    例：已知两数和是10，差是2，求这两个数。
    按口诀，则大数＝（10＋2）/2＝6，小数＝（10－2）/2＝4。

    2.鸡兔同笼问题

    【口诀】
    假设全是鸡，假设全是兔。多了几只脚，少了几只足？除以脚的差，便是鸡兔数。

    例：鸡免同笼，有头36 ，有脚120，求鸡兔数。
    求兔时，假设全是鸡，则免子数＝（120－36×2）/（4－2）＝24
    求鸡时，假设全是兔，则鸡数 ＝（4×36－120）/（4-2）＝12

    3.浓度问题

    （1）加水稀释

    【口诀】
    加水先求糖，糖完求糖水。糖水减糖水，便是加糖量。

    例：有20千克浓度为15％的糖水，加水多少千克后，浓度变为10％？
    加水先求糖，原来含糖为：20×15％＝3（千克）
    糖完求糖水，含3千克糖在10％浓度下应有多少糖水，3/10％＝30（千克）
    糖水减糖水，后的糖水量减去原来的糖水量，30－20＝10（千克）

    （2）加糖浓化

    【口诀】
    加糖先求水，水完求糖水。糖水减糖水，求出便解题。

    例：有20千克浓度为15％的糖水，加糖多少千克后，浓度变为20％？
    加糖先求水，原来含水为：20×（1－15％）＝17（千克）
    水完求糖水，含17千克水在20％浓度下应有多少糖水，17/（1－20％）＝21.25（千克）
    糖水减糖水，后的糖水量减去原来的糖水量，21.25－20＝1.25（千克)

    4.路程问题

    （1）相遇问题

    【口诀】
    相遇那一刻，路程全走过。除以速度和，就把时间得。

    例：甲乙两人从相距120千米的两地相向而行，甲的速度为40千米/小时，乙的速度为20千米/小时，多少时间相遇？
    相遇那一刻，路程全走过。即甲乙走过的路程和恰好是两地的距离120千米。
    除以速度和，就把时间得。即甲乙两人的总速度为两人的速度之和40+20＝60（千米/小时），所以相遇的时间就为120/60＝2（小时）

    （2）追及问题

    【口诀】
    慢鸟要先飞，快的随后追。先走的路程，除以速度差，时间就求对。

    例：姐弟二人从家里去镇上，姐姐步行速度为3千米/小时，先走2小时后，弟弟骑自行车出发速度6千米/小时，几时追上？
    先走的路程，为3×2＝6（千米）
    速度的差，为6－3＝3（千米/小时）。
    所以追上的时间为：6/3＝2（小时）。

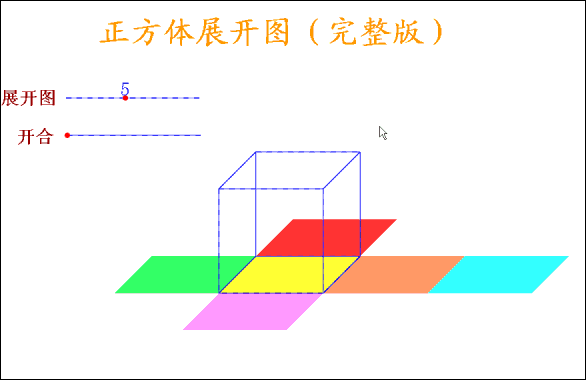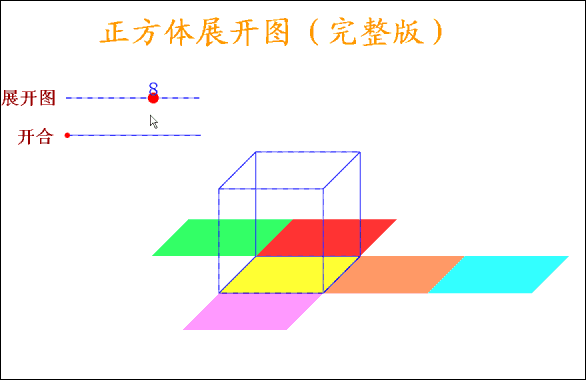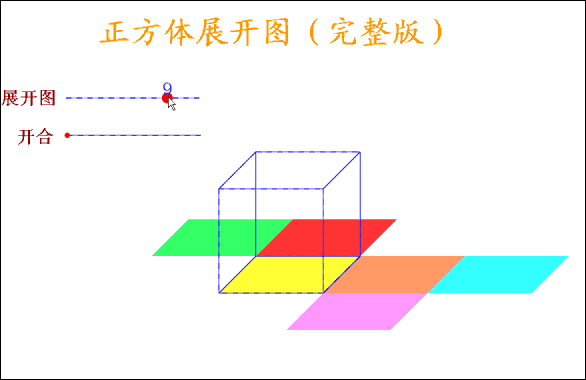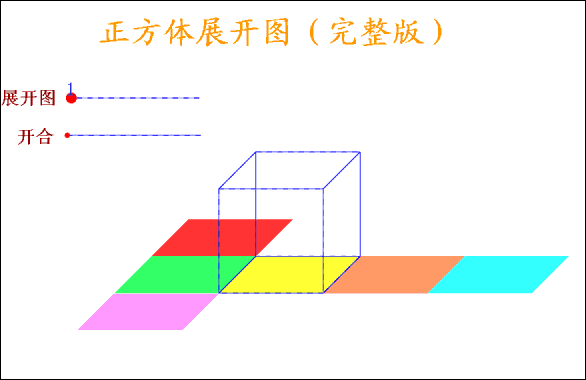
    5.正方体展开图

    正方体有6个面，12条棱，当沿着某棱将正方体剪开，可以得到正方体的展开图形，很显然，正方体的展开图形不是唯一的，但也不是无限的，事实上，正方体的展开图形有且只有11种，11种展开图形又可以分为4种类型：

    1141型：中间一行4个作侧面，上下两个各作为上下底面，共有6种基本图形。

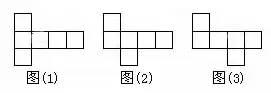
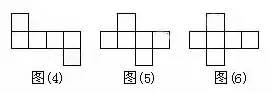
    2231型：中间一行3个作侧面，共3种基本图形。
    3222型：中间两个面，只有1种基本图形。

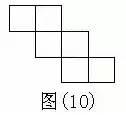
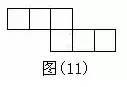
      433型：中间没有面，两行只能有一个正方形相连，只有1种基本图形。

    6.和比问题

    已知整体求部分。

    【口诀】
    家要众人合，分家有原则。分母比数和，分子自己的。和乘以比例，就是该得的。

    例：甲乙丙三数和为27，甲:乙:丙＝2:3:4,求甲乙丙三数。
    分母比数和，即分母为：2＋3＋4＝9；
    分子自己的，则甲乙丙三数占和的比例分别为2/9，3/9，4/9。
    和乘以比例，所以甲数为27×2/9＝6，乙数为：27×3/9＝9，丙数为：27×4/9＝12。

    7.差比问题（差倍问题）

    【口诀】
    我的比你多，倍数是因果。分子实际差，分母倍数差。商是一倍的，乘以各自的倍数，两数便可求得。

    例：甲数比乙数大12，甲:乙＝7:4，求两数。
    先求一倍的量，12/（7－4）＝4，
    所以甲数为：4×7＝28，乙数为：4×4＝16。

（湖南省鼎城区浦沅实验学校 毛敏慧老师推介）