● 对典型应用题回归现象的认识

 

    1.典型应用题回归是对“新大纲”和“实验稿”两个时期教材编排体系特点的调和

 

    就应用题编排而言，“新大纲”时期的教材严格按“式题→文字题→应用题”的递进关系编排，而且应用题内部数量关系的“循序渐进、环环相扣”特点体现得非常明显，结构严谨。“实验稿”时期的教材不再分设单元编排，不分类型，学生遇到一个应用问题时，不再联系类型思考问题，而必须思考情境中的问题与运算意义的联系，结构相对比较松散。

    “实验稿”时期的松散型编排取代“新大纲”时期的严谨型，是基于传统教材题型单一、类别繁琐、机械套用等弊端而作出重要调整。实践证明，“实验稿”时期教材又过于放大情境性和自我性，必要的数量关系、应用题结构没有有序建立，分析应用题方法没有得到应有的训练，学生解决问题能力并没有得到如期的发展和提高。应用题教材编排体系结构从“新大纲”时期的严谨型到“实验稿”时期的松散型，再到“修订稿”时期的调和型，彰显着教材编写者理性的辩证思考态度，是对实际教学的尊重和传统教材优势的吸收。

 

    2.典型应用题回归是充分落实2011版课标新理念的需要

 

    2011版课程标准新增了“抽象”、“推理”、“模型”三个基本数学思想。教学新理念的落实需要抓手，典型应用题就充当了重要的角色。如“工程问题”本质上就是让学生抽象到单位“1”来分析和解决问题，强调了抽象的思想；又如估算策略解决问题的推理过程本质是不等式模型。模型思想是学生体会和理解数学与外部世界联系的基本途径，需要让学生完整经历“问题情境——建立模型——求解验证”的数学活动过程来体会。无论是模型思想作用的感知还是建模过程的体会，应用题是各类学习素材的主导材料，而典型应用题更能反映其独特的结构特点，成为主导中的主导。从某种程度上说，典型应用题的回归是落实数学基本思想的唤求。

 

    3.典型应用题回归是构建应用题结构体系的不可或缺的重要一环

 

    应用题的分类有两个维度，一是根据步数可分为一步应用题、两步应用题和多步应用题，二是根据难易程度可分为一般应用题、复合应用题和典型应用题。从整个应用题结构体系来说，一步应用题是基础，两步应用题是关键，它处在运算意义内化巩固、数量关系基本建立、解题策略初步形成的枢纽环节；三步应用题更多是强调数量关系结构的感知，减少学生记忆应用题类型。

    如在两步应用题中，归总问题是基于“每份数×份数=总数”“总数÷每份数（份数）=份数（每份数）”数量关系提炼，通过画图策略分析凸显“总量不变”这一中间问题的寻找、分析过程，强调综合、分析法的运用。而在三步应用题中，以总数不变作为主体数量关系的归总结构（反比例）是三步数量复合关系基本结构之一。简单地说，归总问题对于整个应用题结构体系的构建而言，是不可或缺的。

 

    4.典型应用题回归是一种传承精华、开拓创新辩证式的扬弃

 

    修订版教材中典型应用题回归是对传统应用题辩证认识的重要标志，是基于传承精华、开拓创新的立场，绝非简单的重走回头路。传统应用题关注问题结构，强调数量关系分析讲解和专项训练，解题模式比较规范固定，这些都有助于应用题结构特征的感知和数学模型的建立。新教材问题解决呈现方式多样，信息多余，强调解决问题策略和表征交流，注重检验反思，有助于发现问题、提出问题、分析问题和解决问题能力的整体贯彻。

    典型应用题回归，并不是传统教材的简单复制，它在保持原有结构基础上增添了许多新元素。比如，归一问题强调了画图分析，并将正反归一合为一课时，跳出了一课一例的禁锢；又如，工程问题融入了赋值计算的假设法，使学生在与整数应用题比较中发现具体总量未知，提出问题后进而讨论得出假设策略，并抽象出假设总量为单位“1”，在数量关系分析中打通整数、分数应用题结构的内在联系，充分经历了发现问题、提出问题、分析问题、解决问题的全过程。

 

    ● 对典型应用题回归现象的思考

 

    1.合理把握教学要求，开展必要的策略指导

 

    由于典型应用题回归不再是简单的复出，而是承载了解决问题策略之类的新要求。教学中，要合理把握教材意图，切勿随意拔高或降低教学要求。比如，用假设法解决工程问题，要体现解决问题方法的多样性和开放性，尽管鼓励学生抽象到单位“1”来解决，但未作硬性要求，允许学生借助具体量的假设解决工程问题；同时在工程问题变式拓展上没有作出更高要求，只需掌握基本类型。又如，归一问题新增了画图策略，教学调查显示学生即使不画图也能顺利解决问题，但此处的画图训练主要是为了画图意识的形成和画图方法的指导，不可贪图省事导致画图策略训练丧失良机。在画图要求上，重直观、重表达，允许不同学生画不同的图。

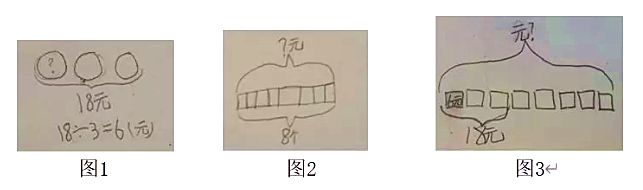
    作为解决问题的策略，是需要教方法的。策略好似一层窗户纸，需要学生来捅，但未必能自行捅破，有时需要教师出手相助或作出针对性指导。比如，用假设法解决工程问题，当学生面临具体总量未知的困难，有些班级全体学生无人想到假设策略，此时需要教师来点破。又如，在归一问题“妈妈买3个碗用了18元，如果买8个同样的碗，要用多少钱？”用图示表征信息、问题时，对各种层次的学生作品（见下图）要进行沟通指导：图1、图2很显然没能全面反映信息和问题，图3用一幅图进行表达，图4用实物图案来表达，图5用方块表达，图6用线段图表达。教学中，要引导学生在读图基础上比较交流，明确画图要全面反映关键信息，要尽可能简洁易懂；同时在后四幅图共性比较中发现“同样的碗”这条信息的表达要点。

 

    2.放眼大局，加强近远景目标的序列训练

 

    不论是画图策略的形成还是数量关系的建立，都有赖于周期性的序列训练，这就需要教师树立整体意识，放眼大局，合理把握近景目标和远景目标要求，有机开展针对性训练。

    比如线段图是归总应用题的题意表征、数量关系分析的主要抓手，也是第二学段分数、百分数应用题分析的通用手段。线段图正式出现是在“倍”的认识，作为解决问题策略则在归总问题正式使用，两者之间存有归一问题画图的过渡。而归一问题画图大多学生停留在离散量的实物替代图水平，与归总问题的连续量线段图是有跨越的，需要教师在归一问题教学时适度介入线段图，为归总问题做好近景目标的准备。而整个小学阶段画图训练这一远景目标，可以作出这样的规划：一至二上，图文应用题的识别；二下，直条图识别，初步学画部整关系直条图；三上，比较关系的线段图识别和学画；四年级，学会简单的线段图；五、六年级，学会稍复杂的线段图。

    而工程问题所依据的基本数量关系“工作效率×工作时间＝工作总量”，教材是没有明示的，从系统角度来看，教师需要适时加以补充渗透。比如在四上“单价×数量＝总价”、“速度×时间＝路程”数量关系学习时进行扩展，为六年级工程问题学习做好必要的准备。