小学数学尺规作图教学中核心素养培育的“三讲究”
《义务教育数学课程标准(2022年版)》在实例“用直尺和圆规作等长线段”部分指出:让学生通过几何作图的方法,在操作过程中形成对几何图形的感觉,感受两点确定一条线段的意义:体会用直尺可以确定直线,用圆规的两脚可以确定线段的长短。教学中应如何落实这一课标要求,引导学生用无刻度的直尺(或不看直尺上的刻度)和圆规,作一条与给定线段长度相等的线段,感受“尺”和“规”的相互作用,理解尺规作图的基本原理和本质,培育数学核心素养呢?
笔者经过课堂教学实践,认为可以从以下三方面入手。
一、在比较线段长短中讲究移一移、画一画,助推理意识的培育
无刻度的直尺和圆规对学生来说是新接触的学习工具,学生对“尺”和“规”在作图中的作用还一知半解。如何让学生在尝试中感受无刻度的直尺虽然不能测量,但可以画直线,以及圆规可以确定线段的长短呢?
笔者认为,在让学生比较线段长短的过程中,可以借助圆规把要比较的线段进行迁移,与其他线段重叠后再比较,并引导学生思考:为什么线段可以迁移?迁移后线段的长度变了吗?为什么?还有其他相等的线段吗?如果有,请画出来。
待学生画完后继续追问:这样的线段能画出几条?为什么?为什么所画出的这些线段的长度都相等?这样,通过移一移、画一画,让“尺”和“规”的作用得到彰显,学生的推理意识也在说理论证中得到了很好的培养。
课堂实践中,笔者首先创设班里有三名学生参加学校实心球队选拔的情境,并出示三名学生的选拔成绩(图1),思考如何判断这三名学生能否进入校队,从而引出任务一“用尺规比较线段的长短”,放手让学生尝试比较。
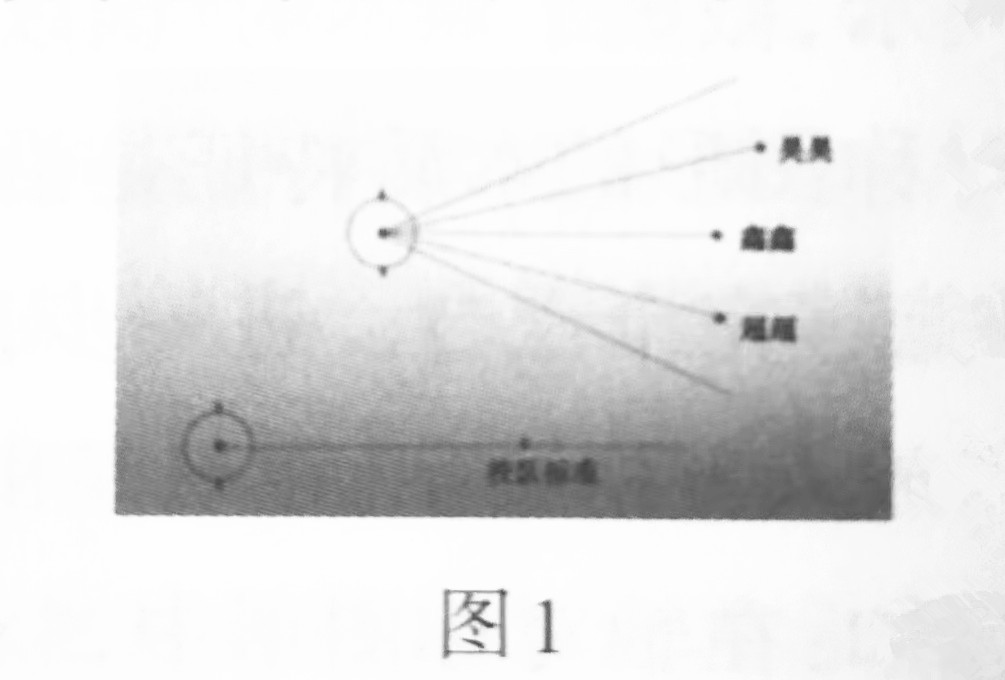
有的学生把圆规的两脚张开,先确定表示校队标准线段的距离,再保持圆规两脚张开的程度不变,分别移动到表示三名学生成绩的线段处,用圆规依次画出三段短弧后进行比较(图2);
有的学生把圆规的两脚张开,先分别确定表示三名学生成绩的线段的距离,再移动到表示校队标准的线段上,同样用圆规画短弧作标记,最后根据校队标准线上三段短弧的位置比较线段长短(图3);
也有的学生把圆规的两脚张开,先确定表示校队标准线段的距离,再把圆规的针尖与表示三名学生成绩的线段的交点重合,直接画出一条长弧后进行比较(图4)。
展示三种画法后,引导学生对比分析,重点思考:只画一条长弧可以吗?为什么?接着,让学生在图上继续寻找并画出与校队标准线段,能画几条就画几条(图5),最后引导学生围绕“为什么可以画出无数条?为什么这无数条线段的长度都相等”进行说理。
如此,让学生在移一移、画一画中经历用尺规比较线段长短的全过程,深刻感受尺规的作用,理解把圆规的两脚张开表示出线段长度后,圆规两脚张开的程度在移动过程中始终保持不变,因此交点到长弧上任意一点间的距离都相等,而弧上有无数个点,所以可以画出无数条等长线段。学生在边操作边说理的过程中,有效发展了推理意识
二、在作等长线段中讲究量一量、验一验,助几何直观的培育
用尺规作等长线段是小学阶段学习尺规作图的伊始,也是后续进一步学习的基础。教学时引导学生理解尺规作图的基本原理,感受“画图”和“作图”虽只有一字之差,要求却不尽相同。画图只需简单描摹出图形的大致样子,而作图则要求有序、规范、精准。
笔者认为,在学生用尺规画出等长线段后,可以让他们借助有刻度的直尺分别量出给定线段与所画线段的长度,将数据进行对比,以验证用尺规作等长线段的准确性。即:让学生在量一量、验一验的过程中直观感受用尺规作图的精准性,培养几何直观。
任务一完成后,学生已经积累了在多条线段上“截”出等长线段的经验,紧接着出示任务二“请你画一条线段CD,使它的长度和线段AB相等”,并放手让学生尝试完成。
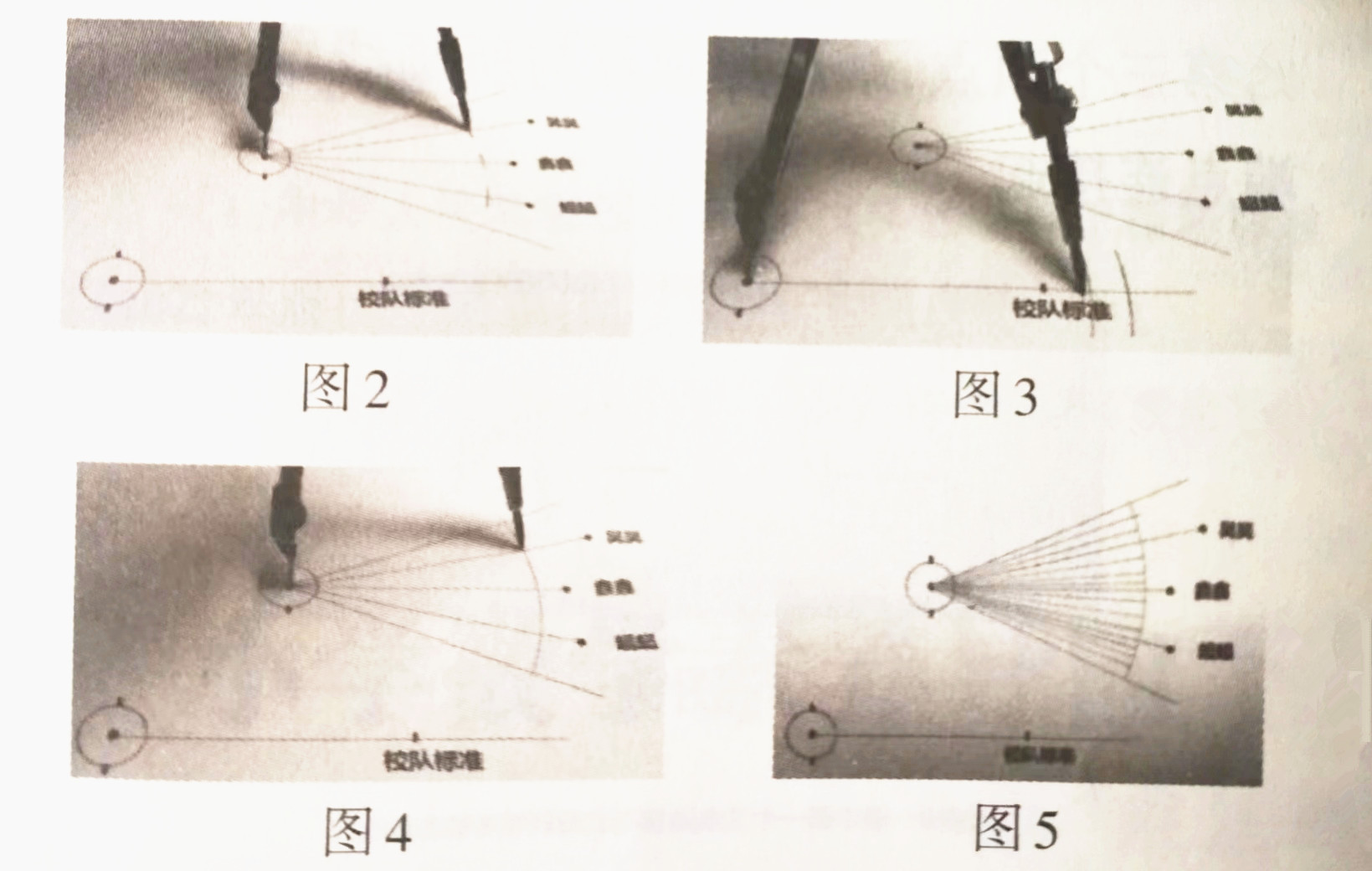
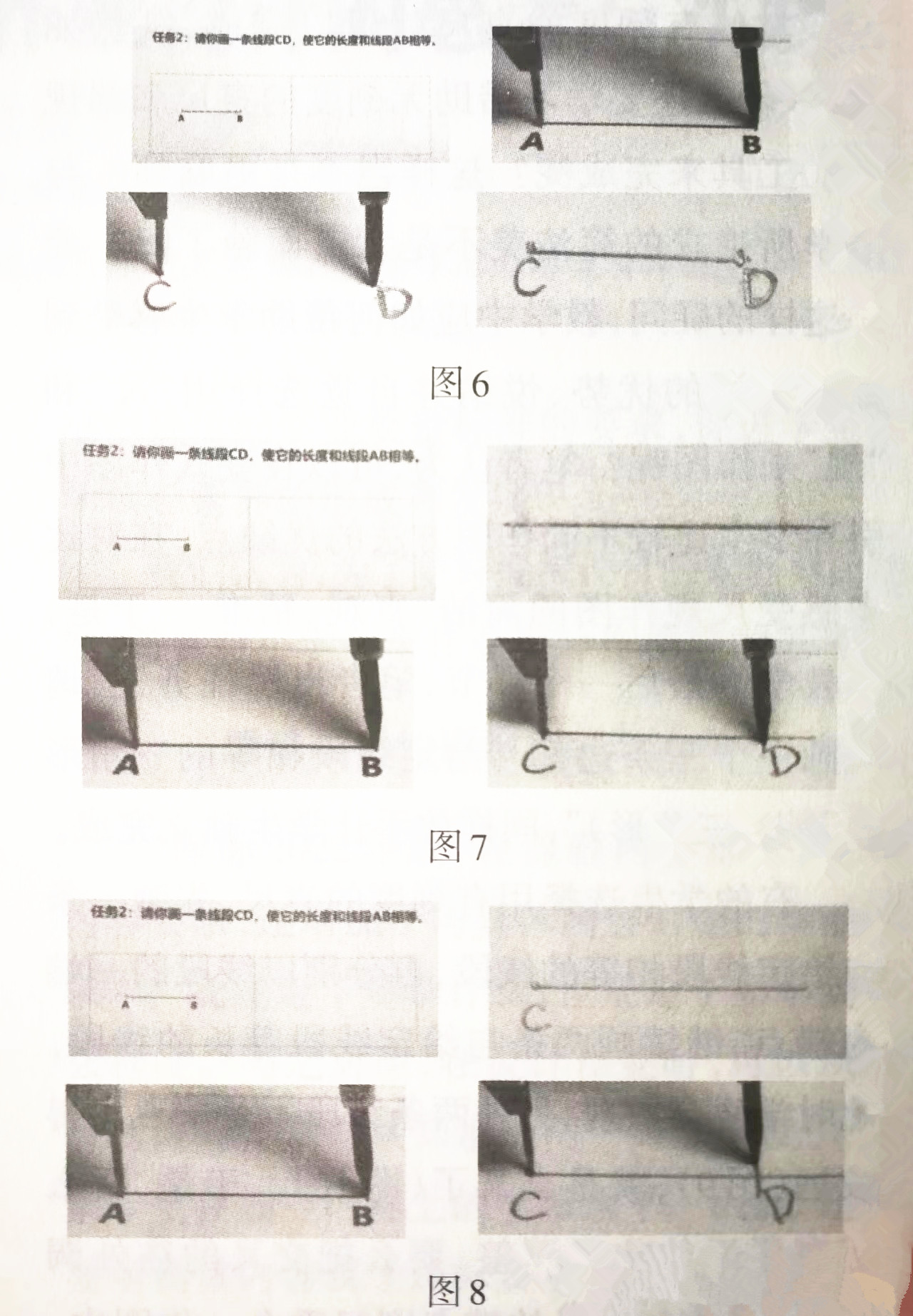
有的学生选择用有刻度的直尺作图,先用直尺测量线段AB的长度,再画一条跟AB一样长的线段,最后标上字母C、D:有的学生选择借助尺规,先用圆规“量”出线段AB的长度,在保持圆规两脚间距离不变的情况下,把圆规移动到空白处,再分别在圆规的针尖和笔尖处标记点C、点D,最后用尺子连线(图6);
也有的学生先画一条直线,再用圆规“量”出线段AB的长度,然后在直线上截取和线段AB一样长的线段,并在针尖和笔尖处标记点C、点D(图7);
还有的学生先画一条射线,并在射线的端点处标记点C,再用圆规“量”出线段AB的长度,接着把圆规针尖与点重合,在射线上画出短弧并标上点D(图8)……
最后师生交流并优化作图方法。
如果教学仅停留于此,学生对尺规作图的掌握只会局限在机械操作的技能层面,无法直观体会到尺规作图的精准性,明白尺规作图的基本原理。因此,笔者进一步启发学生思考:用尺规作出的线段CD与线段AB相等吗?如何验证?学生利用有刻度的直尺分别测量出线段AB和线段CD的长度,再进行比较,在测量与验证中深刻体会尺规作图的准确性,进一步理解了圆规的两脚在这个过程中所发挥出的度量作用和定长作用,也明白了尺规作图的基本原理。其间,学生的思维也逐步从具体向抽象转化,有助于几何直观能力的培养。
三、在变式作图中讲究比一比、辨一辨,助思维品格的培育
知识的形成一般需要经历同化、顺应的过程。比较线段长短、作等长线段等内容借助以前学过的有刻度的直尺就可以完成,既然如此,为什么还要学习借助无刻度的直尺和圆规两种工具来完成呢?这样岂不是更麻烦?与数学所追求的简洁美不是背道而驰了吗?
面对这样的疑问,教学中应如何帮助学生感受到尺规作图的优势,悦纳并自觉选择用“尺”和“规”来作图呢?
笔者认为,可以在变式作图中引导学生比较不同作图方法的优缺点,在对比中感受尺规作图的简洁、直观、精准。于是,在教学的最后一个环节,笔者出示任务三“请你画一个三条边都与给定线段相等的三角形(即等边三角形)”,同样放手让学生独立完成。
有的学生选择用有刻度的直尺,先画一条与给定线段相等的线段,再分别以线段的一端为端点,继续画两条与给定线段等长的线段。
此时学生会发现,另外两条线段不是端点离得较远(图9),就是交叉了(图10)。于是,要么把离得远的往里调整,要么把交叉的往外调整,直至两条线段的端点刚好重合。作图中,我要求学生保留调整痕迹,便于后面进行比较。
也有的学生选择用无刻度的直尺和圆规来画,先画一条与给定线段相等的线段,保持圆规两脚间的距离不变,再将圆规的针尖分别与线段的一端重合画弧,两条弧相交于一点。这个点就是三角形的第三个顶点,最后用尺子把这个顶点与线段的两个端点连接起来(图11)。
还有的学生选择用有刻度的直尺和圆规作图,先用尺子测量出给定线段的长度,画出一条与之相等的线段,再借助圆规找出三角形的第三个顶点,最后把顶点与所画线段的两个端点连接起来。
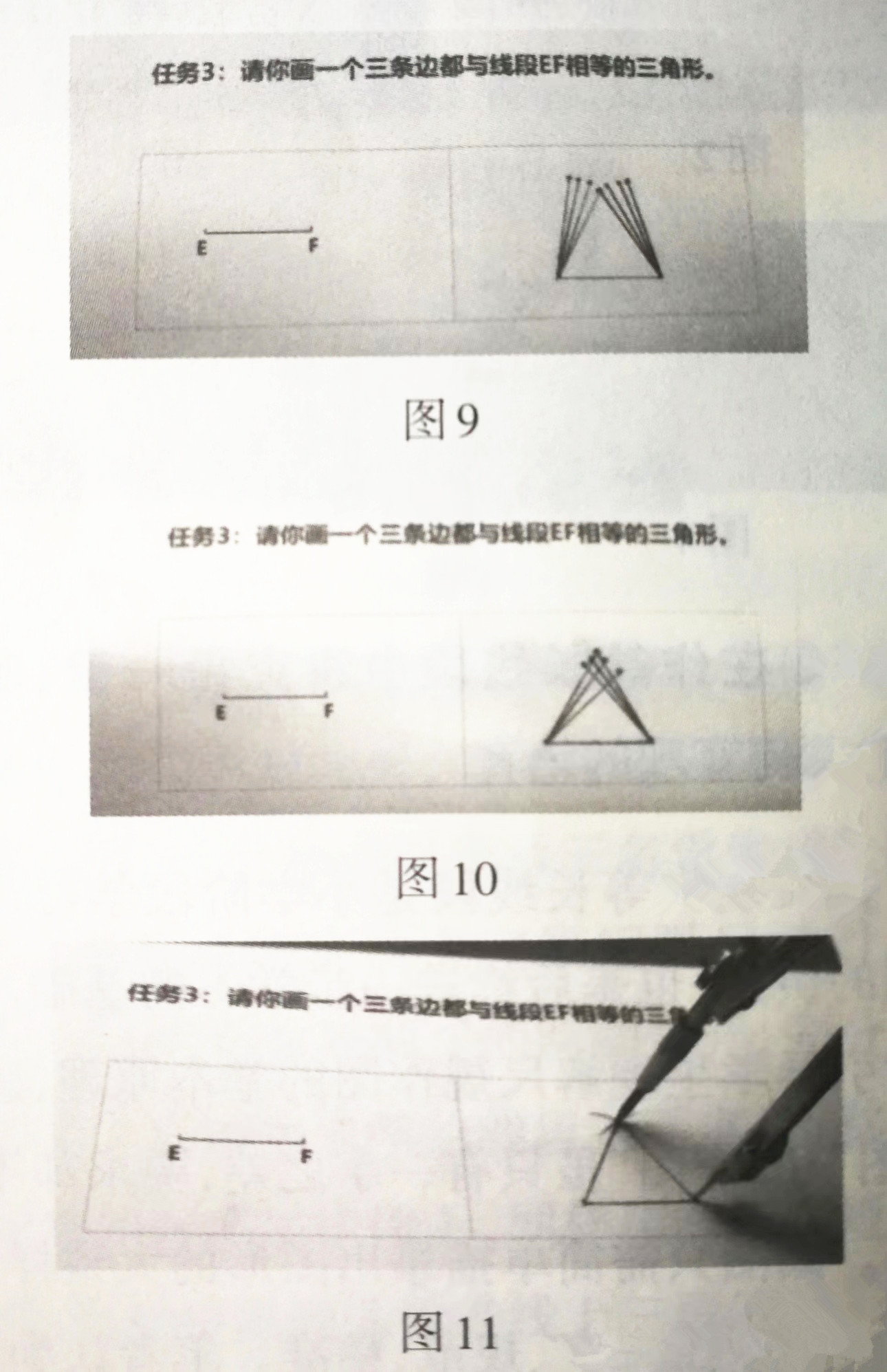
笔者引导学生对比三种方法,借助所保留的作图痕迹,学生一下子就明白了:只借助有刻度的直尺,要想顺利找到三角形的第三个顶点需要进行多次调整,且作图并不一定精准;面借助圆规则无需调整,不管直尺有无刻度,均可快速准确完成作图。
在比一比、辩一辩中,学生不仅进一步夯实了尺规作图的技能,还感受到了尺规作图的简洁性、直观性、方便性,明白了为什么要用尺规作图,思维得到了进一步的提升。
尺规作图植根于几何图形的内在特征和图形之间的联系,作图的过程不仅仅是一种操作,更是数学探究和思维的过程,是联系、重构、内化几何知识的过程。作为一名小学数学教师,应充分探索尺规作图的教学实施路径,发掘其教学价值,让学生在玩中学、做中学、创中学,积累活动经验,培养几何直观、推理意识和数学思维品格,最终实现数学核心素养的培育。
顶一下
(1)
50%
踩一下
(1)
50%
上一篇:关于尺规作图的解读与教学建议
下一篇:没有了
- 发表评论
-
- 最新评论 进入详细评论页>>