小学数学思想方法(5)——方程和函数思想

1.方程和函数思想的概念
方程和函数是初等数学代数领域的主要内容,也是解决实际问题的重要工具,它们都可以用来描述现实世界的各种数量关系,而且它们之间有着密切的联系,因此,本文将二者放在一起进行讨论。
(1)方程思想
含有未知数的等式叫方程。判断一个式子是不是方程,只需要同时满足两个条件:一个是含有未知数,另一个是必须是等式。如有些小学老师经常有疑问的判断题:χ=0 和χ=1是不是方程?根据方程的定义,他们满足方程的条件,都是方程。
方程按照未知数的个数和未知数的最高次数,可以分为一元一次方程、一元二次方程、二元一次方程、三元一次方程等等,这些都是初等数学代数领域中最基本的内容。方程思想的核心是将问题中的未知量用数字以外的数学符号(常用χ、y等字母)表示,根据相关数量之间的相等关系构建方程模型。方程思想体现了已知与未知的对立统一。
(2)函数思想
设集合A、B是两个非空的数集,如果按照某种确定的对应关系?如果对于集合A中的任意一个数χ,在集合B中都有唯一确定的数y和它对应,那么就称y是χ的函数,记作y=f(χ)。其中χ叫做自变量,χ的取值范围A叫做函数的定义域;y叫做函数或因变量,与χ相对应的y的值叫做函数值,y的取值范围B叫做值域。
以上函数的定义是从初等数学的角度出发的,自变量只有一个,与之对应的函数值也是唯一的。这样的函数研究的是两个变量之间的对应关系,一个变量的取值发生了变化,另一个变量的取值也相应发生变化,中学里学习的正比例函数、一次函数、二次函数、幂函数、指数函数、对数函数和三角函数都是这类函数。
实际上现实生活中还有很多情况是一个变量会随着几个变量的变化而相应地变化,这样的函数是多元函数。虽然在中小学里不学习多元函数,但实际上它是存在的,如圆柱的体积与底面半径r和圆柱的高的关系:V=π* r *rh。半径和高有一对取值,体积就会相应地有一个取值;也就是说,体积随着半径和高的变化而变化。
函数思想的核心是事物的变量之间有一种依存关系,因变量随着自变量的变化而变化,通过对这种变化的探究找出变量之间的对应法则,从而构建函数模型。函数思想体现了运动变化的、普遍联系的观点。
2.方程和函数的关系
(1)方程和函数的区别
从小学数学到中学数学,数与代数领域经历了从算术到方程再到函数的过程。算术研究具体的确定的常数以及它们之间的数量关系。方程研究确定的常数和未知的常数之间的数量关系。函数研究变量之间的数量关系。
方程和函数虽然都是表示数量关系的,但是它们有本质的区别。如二元一次不定方程中的未知数往往是常量,而一次函数中的自变量和因变量一定是变量,因此二者有本质的不同。方程必须有未知数,未知数往往是常量,而且一定用等式的形式呈现,二者缺一不可,如2χ-4=6。
而函数至少要有两个变量,两个变量依据一定的法则相对应,呈现的形式可以有解析式、图象法和列表法等,如集合A为大于等于1、小于等于10的整数,集合B为小于等于20的正偶数。那么两个集合的数之间的对应关系可以用y=2χ表示,也可以用图象表示,还可以用如下的表格表示。

人们运用方程思想,一般关注的是通过设未知数如何找出数量之间的相等关系构建方程并求出方程的解,从而解决数学问题和实际问题。
人们运用函数思想,一般更加关注变量之间的对应关系,通过构建函数模型并研究函数的一些性质来解决数学问题和实际问题。方程中的未知数往往是静态的,而函数中的变量则是动态的。方程已经有3000多年的历史,而函数概念的产生不过才300年。
(2)方程和函数的联系
方程和函数虽然有本质的区别,但是它们同属代数领域,也有密切的联系。如二元一次不定方程aχ+by+c=0和一次函数y=kχ+b,如果方程的解在实数范围内,函数的定义域和值域都是实数。那么方程aχ+by+c=0经过变换可转化为y=-(a/b) χ-c/b,它们在直角坐标系里画出来的图象都是一条直线。
因此,可以说一个二元一次方程对应一个一次函数。如果使一次函数y=kχ+b中的函数值等于0,那么一次函数转化为kχ+b=0,这就是一元一次方程。因此,可以说求这个一元一次方程的解,实际上就是求使函数值为0的自变量的值,或者说求一次函数图象与χ轴交点的横坐标的值。
一般地,就初等数学而言,如果令函数值为0,那么这个函数就可转化为含有一个未知数的方程;求方程的解,就是求使函数值为0的自变量的值,或者说求函数图象与χ轴交点的横坐标的值。
3.方程和函数思想的重要意义
16世纪以前,人们主要是应用算术和方程方法解决现实生活中的各种实际问题,方程与算术相比,由于未知数参与了等量关系式的构建,更加便于人们理解问题、分析数量关系并构建模型,因而方程在解决以常量为主的实际问题中发挥了重要作用。
到了17世纪,随着社会的发展,传统的研究常量的算术和方程已经不能解决以探究两个变量之间的关系为主的经济、科技、军事等领域的重要问题,这时函数便产生了。函数为研究运动变化的数量之间的依存、对应关系和构建模型带来了方便,从而能够解决比较复杂的问题。
概括地说,方程和函数思想是中小学数学,尤其是中学数学的重要内容之一。方程和函数在研究和构建现实世界的数量关系模型方面,发挥着重要的不可替代的作用。
4.方程和函数思想的具体应用
小学数学在学习方程之前的问题,都通过算术方法解决。在引入方程之后,小学数学中比较复杂的有关数量关系的问题,都可以通过方程解决,方程思想是小学数学的重要思想,其中一元一次方程是小学数学的必学内容。
在小学数学里没有学习函数的概念,但是有函数思想的渗透,与正比例函数和反比例函数最接近的正比例关系和反比例关系是小学数学的必学内容。另外,在小学数学的一些知识中也会渗透函数思想,如数与数的一一对应体现了函数思想。
方程和函数是小学数学与初中数学衔接的纽带。
小学数学中方程和函数思想的应用如下表。
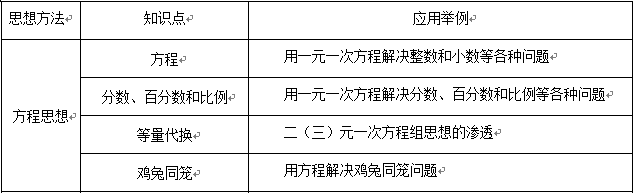
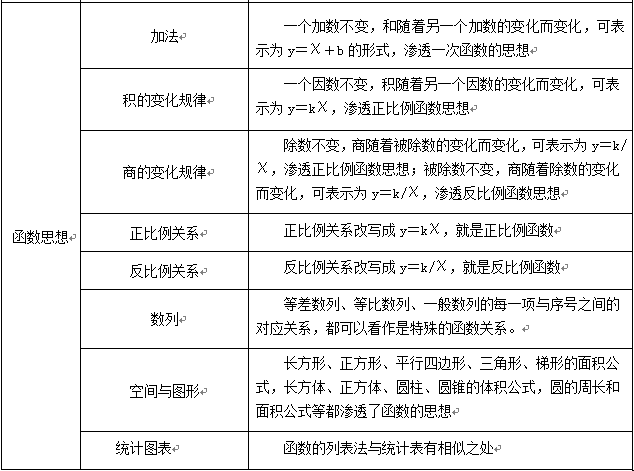
5.方程和函数思想的教学
方程和函数都是义务教育阶段重要的数学思想方法,用方程和函数表示数量关系和变化规律,不仅能体现方程和函数思想的应用价值,也有助于学生形成模型思想。根据课程标准的理念,方程和函数思想的教学应关注以下几点。
(1)方程中的字母χ、y等代表具体的未知的常数,即未知数,这是代数思想和方程思想的基础。
(2)正比例关系和反比例关系等函数关系式中的字母χ、y等代表的是变化的量,即变量,而且这两个量是相关联的量,一个量变化,另一个量会随之变化,这是函数思想的基础。要让学生体会他们的区别。
(3)结合具体情境,通过分析数量关系来理解等量关系,并用方程表示等量关系,再通过解方程解决问题,从而认识方程的作用。
(4)结合简单情境,认识成正比例的量或反比例的量,通过分析数量关系和变化规律建立比例关系式,再通过解比例解决问题。
(5) 能根据给出的有正比例关系的数据在方格纸上画图,并根据其中一个量的值估计另一个量的值。
下面再结合案例谈谈方程和函数思想的教学。
案例1:妈妈买了3千克香蕉和2千克苹果,一共花了16元。苹果的价格是香蕉的2倍多1元,苹果和香蕉的单价各是多少?
分析:题目涉及的是商品的数量、单价和总价的关系,根据数量关系“单价×数量=总价”进行分析,题中出现了两种商品,总价也是两种商品的总价。所以等量关系应为“香蕉的单价×香蕉的数量+苹果的单价×苹果的数量=总价”。再根据这个等量关系找出题中已知的量,总价16元、香蕉的数量3千克和苹果的数量2千克。未知的是香蕉和苹果的单价,也就是题目中要求的量。设香蕉的单价是χ元/千克,苹果的单价是y元/千克。根据题意,可列出如下方程。
3χ+2y=16,y=2χ+1。根据等量代换的原理,两个方程可合并成一个方程,3χ+2(2χ+1)=16。这是在小学数学中遇到含有有关系的两个未知数的方程时能够直接列出一个方程的依据。如和倍、差倍、鸡兔同笼等问题,用方程解决也是利用了这个原理。解方程,χ=2, y=5。
案例2:小明家的果园供游人采摘桃,每千克10元。请写出销售桃的总价(总收入)y元与数量(千克数) χ之间的关系式。如果某天的销量是50千克,这天的总收入是多少?如果上个月的总收入是12000元,上个月的销量是多少?
分析:此题涉及的也是商品的单价、数量和总价的关系,仍然要根据数量关系“单价×数量=总价”进行分析。根据题意,已知的量是单价,未知的量是总价和数量,题目已经告诉我们分别用y和χ表示。因为桃的单价一定,所以它的总价与数量成正比例,可列关系式:y=10χ。某天的销量是50千克,总收入是500元。上个月的总收入是12000元,销量是1200千克。
案例2和案例1相比较,都有两个量分别用y和χ表示。
案例1中的y和χ虽然是未知的量,但是它们实际上是具体的静止的常量,都有一个固定的值,通过解方程可以得到它们的值。
案例2的两个量y和χ则是相关联的变化的量,χ的取值可以是一定范围内 (果园内桃子总质量的最大值以内) 的任何一个数,y随χ的变化而变化。只有y和χ中的一个量取一个具体的值时,另一个量才会相应地取一个具体的值。如案例2中的具体问题的解答。
案例3:有一批捐赠的图书分给一个班的学生,如果每人分3本,则还缺15本;如果每人分2本,则剩余25本。这个班有多少学生?
分析:根据题意,这批书的数量和学生人数都是定值,那么表示书的数量的式子应该相等。题目求的是学生的数量,可设为未知数,书的数量可由学生的数量表示。设这个班有χ名学生,那么书的数量可分别表示为3χ-15和2χ+25,因此,可列方程3χ-15=2χ+25。解方程,χ=40。
案例4:无限循环小数0.777…和0.747474…如何化成分数?你能发现什么规律?
分析:根据小数和分数的关系,有限小数化分数比较容易进行。由于无限循环小数具有位数无限的特点,不能直接用有限小数化分数的方法进行。
根据循环小数的循环节不断重复出现的特点,循环节是几位数字,就把这个循环小数乘10的几次方;它的左起第一个循环节就变成了整数部分,而循环小数部分不会改变;二者的小数部分相同,二者的差为由循环节变成的整数部分。
因此,可利用差倍问题的原理,列方程解决问题。如设χ=0.777…,那么10χ=7.777…,求它们的差,10χ-χ=7,解方程,χ=7/9,所以0.777…=7/9。同理可得,100χ-χ=74,χ=74/99,所以0.747474…=74/99。
无限循环小数化分数的规律是:把循环节组成的数作为分子,循环节有几位数字,分母就是由几个9组成的几位数。
顶一下
(1)
100%
踩一下
(0)
0%
- 发表评论
-
- 最新评论 进入详细评论页>>