人教版六年级上册第五单元“圆”介绍
老师们好:
我是黄老师。
今天,“我读新教材”的内容是——人教版数学六年级上册第五单元“圆”。
一、教学内容
1.圆的认识
2.圆的周长
3.圆的面积
4.扇形的认识
二、教学目标
1.认识圆,学会用圆规画圆,掌握圆的基本特征。
2.会利用直尺和圆规,在教师指导下设计一些与圆有关的图案。
3.通过实践操作,理解圆周率的意义,理解和掌握圆的周长计算公式,并解决一些相应的实际问题。
4.探索并掌握圆的面积计算公式,并解决一些简单的实际问题。
5.认识扇形,掌握扇形的一些基本特征。
6.经历尝试、探究、分析、反思等过程,培养数学活动经验,在解决一些与圆有关的数学问题的过程中,提高问题解决的能力。
7.在推导圆的周长与面积的计算公式过程中体会和掌握转化、极限等数学思想。
8.通过生活实例、数学史料,感受数学之美,了解数学文化,提高学习兴趣。
三、“圆”的主要变化
1.改变圆的各部分名称的引入方式
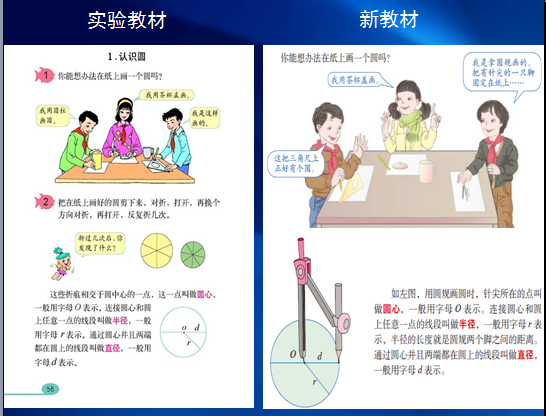
实验教材在引入圆时,先让学生利用圆形杯盖、圆柱体物体、三角板上的圆孔描出圆,再把圆剪下来,通过多次对折等方式引出圆心、半径、直径等概念;在认识了圆的半径和直径的特点之后,再专门教学用圆规画圆的方法。
考虑到学生在生活中已经具备初步的用圆规画圆的知识,新教材对于“你能想办法在纸上画一个圆吗”这一问题,同时给出了用杯盖、三角尺上的圆孔、圆规画圆的方法,符合真实的学情。接下来,利用圆规画圆的方法引出圆心、半径、直径等概念,水到渠成,这样的引入方式也能更好地体现圆“一中同长”的本质特征。
2.增加“圆心决定圆的位置、半径决定圆的大小”的内容

“圆,一中同长也”,这是《墨子》中对圆的定义。只要确定了“中”和“长”,圆的位置与大小就确定下来了。圆心决定圆的位置、半径决定圆的大小这一事实,过去虽然没在教材中明确指出,但实际上学生已经在自觉应用了。在本册教材中,接下来还要安排利用圆设计图案的内容,在设计图案的过程,学生会时时处处遇到“要画一个多大的圆”“这个圆的圆心应该在哪儿”等问题。因此,教材增加这一部分内容,能帮助学生在应用知识的过程中更好地认识圆的数学特征。
3.减少“圆的对称性”的篇幅,增加“利用圆设计图案“的内容
由于在前面“轴对称图形”的相关内容中,已经对圆的对称性有过比较充分的探讨,所以,本单元不再单独编排圆的对称性的例题,只在相关练习中加以巩固。
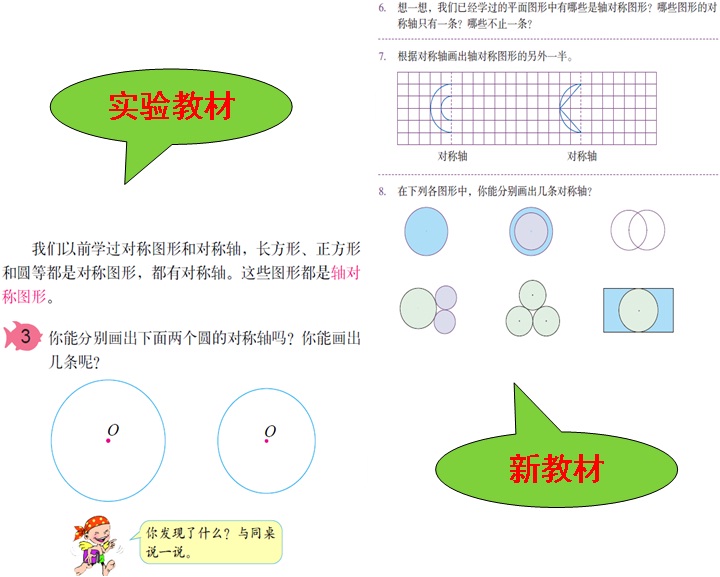
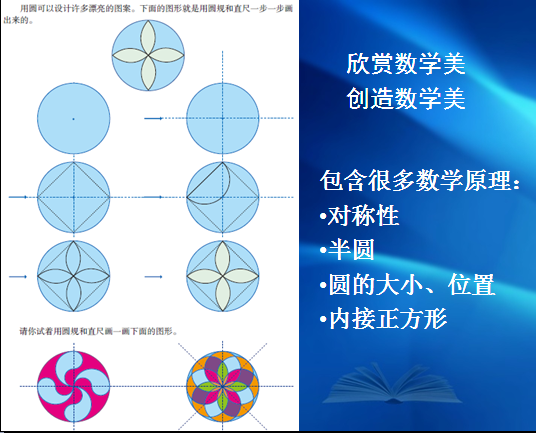
在新教材中,新增了利用圆设计图案的内容。先让学生模仿教材上提供的步骤,画出美丽的图案,再放手让学生试着画出教材上提供的图案。
在这一过程中,需要用到用圆规画圆的方法,需要观察这些图案是由哪些图形组成的,是如何组成的。需要学生对圆心位置的确定、半径大小的确定、圆的对称性等知识加以综合应用,一方面,帮助学生进一步了解圆的特征,另一方面,使学生充分体会数学的对称美、和谐美。

4.增加求圆与外切正方形、内接正方形之间面积的内容
在“圆的面积”部分,增加了例3解决实际问题的内容,即求圆与外切正方形、内接正方形之间的面积。
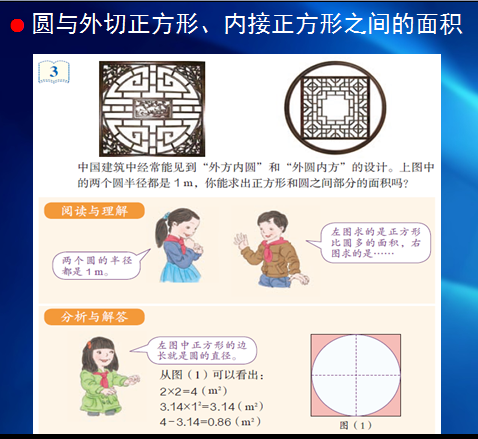
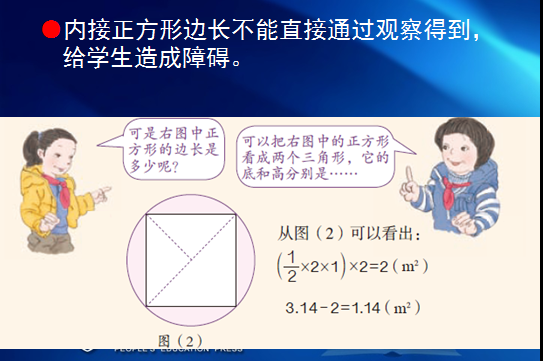

要求学生利用图形之间的关系,灵活计算这两部分的面积,并在“讨论”环节进一步得出更为一般化的结论。
5.“扇形”由选学变为正式教学内容
扇形的内容是学习扇形统计图的必要基础,根据《(2011年版)课程标 准》对相关内容的调整,新教材把这部分内容由实验教材的选学内容变为正式教学内容。这是因为到第七单元学习扇形统计图时,需要用到各部分扇形的大小占整个圆的百分数。当然,这些内容只需要学生直观感知并理解,总体要求并不高。因此,教材上只列出了两类特殊的扇形:半圆为弧的扇形对应的一类圆心角是180°的扇形,即半圆;另一类圆心角是90°的扇形,即四分之一圆。
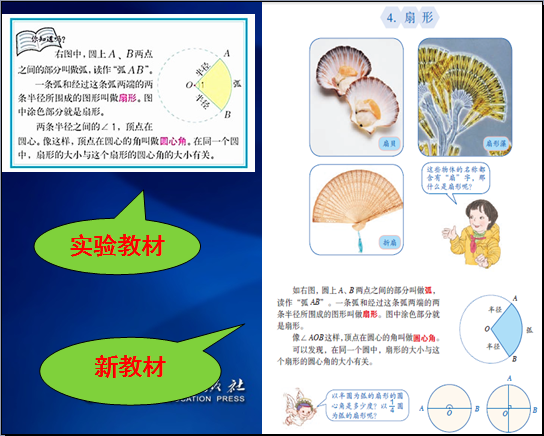
四、教学建议
1.引导学生动手操作、自主探索圆的特征
实际教学时,教师应注意多让学生动手操作,通过画一画、剪一剪、围一围、拼一拼等多种形式,帮助学生认识圆的基本特征。

当然,教师不应简单地把学生的动手操作作为活动目的,而应该引导学生以动手操作为基础,探索和发现圆的有关特性。如此,学生不仅掌握了知识和技能,体验到了操作活动的价值,还有效地积累了数学活动的经验。

2.注重引导学生运用和体验转化、极限等数学思想方法
本单元中涉及许多数学思想方法,教学时,应将此作为一个重要的教学目标予以落实。

比如圆的周长计算公式的推导,就用到了转化的思想,我们需要引导学生深入地去体会这种思想方法。教学时,要让学生认识到转化是一种很重要的数学思想方法,人们常常把复杂转化为简单、把未知转化为已知,来解决日常问题和进行科学研究。
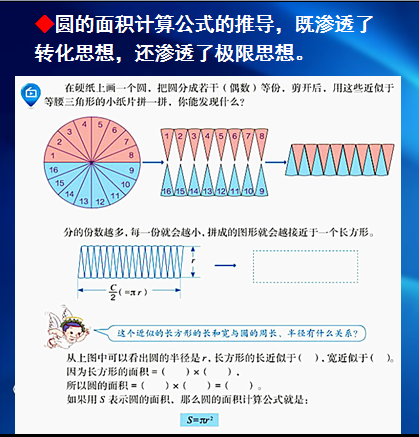
在推导圆的面积计算公式时,不仅用到了转化思想,还渗透了极限思想。将圆分成16等份,能拼成一个近似的长方形,教师可以充分利用信息技术手段,展示等分成32份、64份甚至更多份的情况,让学生直观地看到图形的变化趋势。在此基础上引导学生想象:若分的份数无限增加,最后会是怎样的情况?
3.紧密结合生活素材,培养学生在日常生活中应用数学的意识和能力
因为圆在生活中有着广泛应用,所以研究圆的时候,学习材料可以从生活中来,研究得到的结论可以反过来应用于生活。在教学中,要合理用好生活素材,把这些素材作为引发学生探究、促进学生思考、加深学生感悟的有效载体。
在学习新知时,要善于从生活素材中引出。学生对熟悉的材料会有亲近感,会有探究的兴趣。


在知识应用时,教师要及时以生活素材为例,让学生尝试运用所学知识去解释(或解答),以达到巩固知识、加深体验、学以致用的目的。



这样,学生就有更多的机会从周围熟悉的事物中学习数学和理解数学,学生眼中的数学也就不再是简单的数学公式,而是富有情感、贴近生活、具有活力的科学。
以上是我对这一单元的一些不成熟的思考和体会,不当之处,敬请指正。
谢谢大家!
●温馨提示:您想观看该内容的教学视频,请链接——http://txm.dj1978.com/a/keqianzhunbei/jiaocaijiedu/jiaocaijiedushipin/li/20150518/523.html
●温馨提示:您想下载该内容的教学课件,请链接——http://txm.dj1978.com/a/woduxinjiaocaikejian/six2/2015/0519/537.html
●温馨提示:您想观看该内容的教学视频,请链接——http://txm.dj1978.com/a/keqianzhunbei/jiaocaijiedu/jiaocaijiedushipin/li/20150518/523.html
●温馨提示:您想下载该内容的教学课件,请链接——http://txm.dj1978.com/a/woduxinjiaocaikejian/six2/2015/0519/537.html
顶一下
(0)
0%
踩一下
(0)
0%
上一篇:没有了
- 发表评论
-
- 最新评论 进入详细评论页>>