数学核心素养视角下“图形与几何”专题活动设计例谈

审视 聚焦 创新
——数学核心素养视角下“图形与几何”专题活动设计例谈
摘要:
本文以“图形与几何”领域为例,论述如何在数学核心素养的视角下审视常见的问题,以扬弃的目光聚焦于知识与技能中内隐的思想方法、活动经验、理性思考等学科素养,拓延成系列富有新意的专题活动。
关键词:
核心素养 专题活动 等积变形 空间观念 多元融合 逻辑推理
当前,核心素养已成为教育理论研究与教育规律探索的中心议题,而学生核心素养的培养最终要落实在学科的核心素养上。笔者以“图形与几何”领域中常见的问题为例,审视其内隐的价值,聚焦可挖掘与深化的数学素养,拓延成系列富有新意的专题活动,真正促进学生数学素养的提升。
一、形变位移,渗透等积变形
“图形与几何”的实际运用中,常会出现求图形阴影部分面积的运算,以此检测学生对面积公式运用的熟练程度。当出现需通过图形运动转化成学过的规则图形,从而快速求解的题目时(图1),学生的思维往往被激活。
认真审视这些题型可以发现,平常教学更加关注解决这类问题的方法、策略及技能的训练,对蕴含其中的“等积变形”思想体验却不够深入。
设计以“形变位移”为主要内容的专题活动,在动手操作、动眼观察与动脑思考中渗透“等积变形”的思想,能深化认知,感悟数学思想的魅力,形成灵活变通的数学思维。
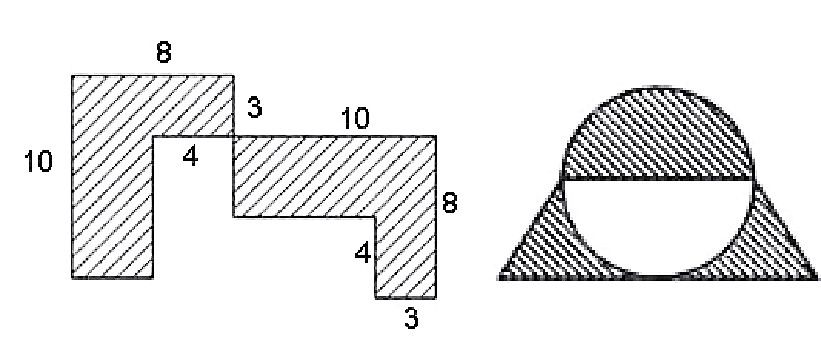
图1
“等积变形”专题活动
(一)拼一拼
1.把一张正方形纸均分成大小和形状完全相同的4份,它们可以拼成学过的平面图形,你能拼出几种?

2.学生尝试, 展示以下几种拼法。

3.学生说一说怎么分类,最后聚焦以“是否有空隙”为标准的分法。
4.在两类图形的比较中,学生明晰:有空隙的图形面积发生改变,密铺的图形形状变了,面积大小不变。这就是数学中的“等积变形”。
(二) 证一证
1.出示:大圆的半径是小圆的2倍,大圆的面积是小圆的 ( ) 倍。
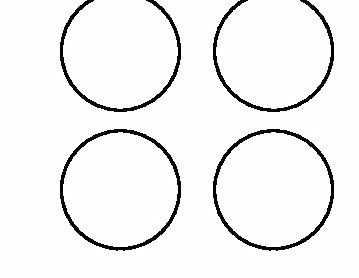

2.用图形直观证明它们之间的关系。学生把四个小圆切割后拼成近似的平行四边形,与大圆切割后拼成的平行四边形比较(图2),发现面积相等。教师适时点明这是“化曲为直”的方法。
3.如何直接用四个小圆拼成一个大圆呢?师生合作共同完成(如图3, 一个小圆平均分成24份,两个小圆平均分成12份,另一个小圆放在正中间,拼成一个大圆,拼成的大圆与原来的大圆完全重合)。教师点明这是“化曲为曲”的证明方法。
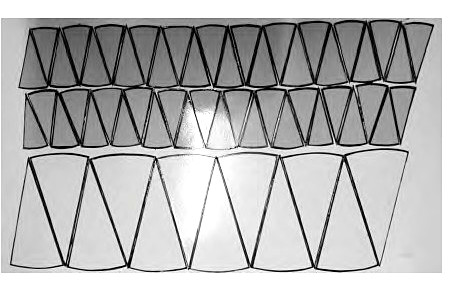
图2

图3
在用四个不规则四边形拼组平面图形的活动中,通过位置移动再现正方形、长方形、平行四边形、梯形,富有挑战又突破常规。学生在等积与不等积变形的对比中明晰概念,形成直观表象。后继直观证明活动,既联系学生已有的“化曲为直”转化经验,又创造性地“化曲为曲”直观验证, 超越学生已有认知,产生震撼的神奇感与美感。
二、面体转化,发展空间想象
“能由实物形状想象出几何图形,由几何图形想象出实物形状”是空间观念的重要内涵,也是几何领域解决问题的重要能力。然而,限于年龄和知识基础,小学生在二维平面再现三维图形的能力较差。
基于此,可以设计以“面体转化”为主要内容的专题活动,让学生在层层推进的平面与立体变换中体验神奇、感受美,发展空间想象能力。
“平面与立体变换”专题活动
(一)分一分
1.把下面的六边形分割成三个平行四边形。


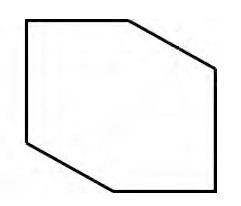
2.学生尝试, 展示作品。
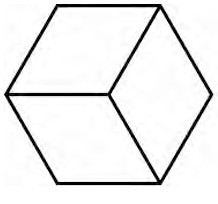
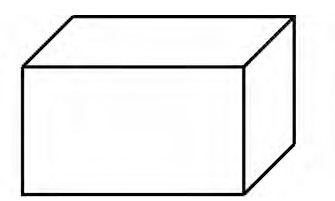
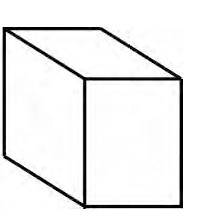

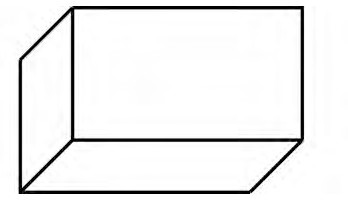
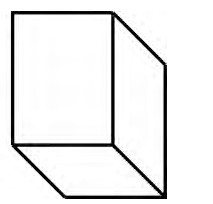
3.揭示:把一个六边形分成三个平行四边形,涂上颜色后平面图形就有立体效果。出示图4,说一说,分别看到长方体的哪些面?揭示:不同的切分方法就像站在不同角度观察长方体,从而看到不同的面。
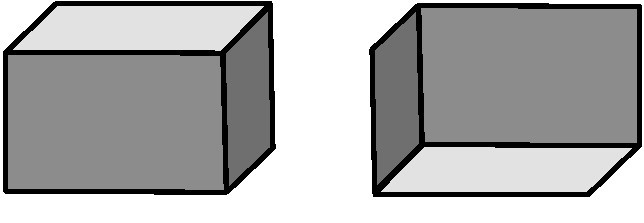
图4
(二)看一看
1.出示一个由平行四边形组合而成的图案(图5),说一说从图案中看出了什么。
学生看出这个图案由平行四边形组成,还从中看到不同的立体图形。 (图6)
2.把图5继续平铺下去形成图7,变换上面的涂色形成图8,让学生感受到明明是平面图形,却隐隐约约有了空间形式。

图5
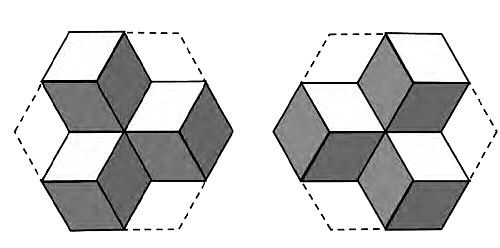
图6

图7
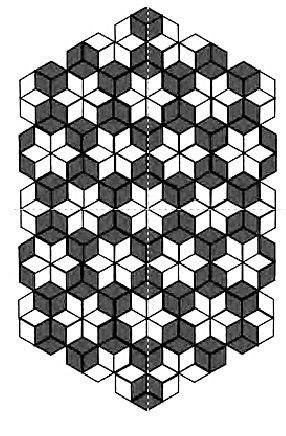
图8
在二维平面画出具有立体效果的图形,对小学生来说是有难度的,在平面图形上感受三维的立体效果却又是神奇的。
“平面与立体变换”的专题活动,让学生在画平行四边形的过程中经历由平面到立体的对比,带来强烈的视觉冲击。学生穿梭在平面与立体的变换里,看似难以相信却又真实存在,这就是空间想象的魅力。
三、突破常规,实现多元融合
数学通过抽象、推理建立模型,使问题解决更加便捷。但是,实际运用模型的过程不是一成不变、固定僵化的,需要根据条件灵活变通,甚至是打破常规、另辟蹊径,合理解决问题。
在“图形与几何”领域设计超越学生常规思维的专题活动,能帮助学生打破固有思维,提升综合素养。
“创意挑战”专题活动
(一)创意分割
1.常规分法
把一张正方形纸分成两块,大小与形状都相同,你能想出几种分法?
学生呈现下列常规分法。

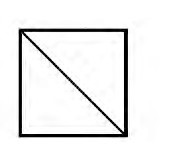
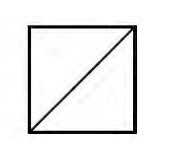
2.分法拓展
启发学生斜线分割,观察发现斜线要经过中心点,且分成的两部分相对称。

3.创意分法
启发学生想出曲线与折线创意分法。
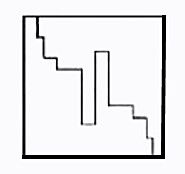
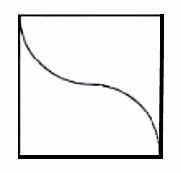
4.关注本质
这么多种分法有什么相同的地方?
引导学生发现:都经过中心点,且两部分的形状相同。适时点明:思考问题时,只要抓住不变的关键,就可以有创意无限的变化。
(二)连续等分
1.操作
把一张正方形纸二等分,把其中的一份再进行二等分,以此类推,连续分五次。
学生尝试,出现以下几种分法。引导学生聚焦有序的分法,养成有序画图的习惯。

2.数形对照
以有序分法为例,假设最小的一份为1,发现图形对应的数列是1、2、4、8、16……若以整个正方形为1,则图形对应的数列是1、1/2、1/4、1/8、1/16……
(三)创意组图
1.变一变
把题(二)中具有数列规律的图形变一变,能组成富有创意的图案。
2.悟一悟
畅谈欣赏图形变化后的想法,感悟数学家庞加莱的名言:感觉数学的美,感觉数与形的协调,感觉几何的优雅!
从常规的直线均分,到斜线均分,直至曲线、折线均分,每一次推进都在“情理之中,意料之外”,仿佛“山重水复疑无路”,却是“柳暗花明又一村”,这是突破常规思维的魅力之所在,也是培养学生创新能力的有效手段。
连续均分活动中,既蕴含有序思维,又有数与形的结合,更融入了艺术创作、文学修饰,学生领悟到数学的美、数与形的协调,以及几何的优雅。
四、以简驭繁,发展逻辑推理
老子曰:“天下难事,必作于易;天下大事,必作于细。”解决复杂问题可以从简单情况想起,发现规律进而“由易及难”。审视“空间与图形”教学,基于“以简驭繁”思想进行的专题活动较少,选择合适的素材让学生深入感悟这一思想方法,能有效提高学生的数学素养。演绎论证中,感悟变化的内在统一性,享受“由易及难”思考的神奇魅力。
“以简驭繁”专题活动
(一)激活旧知
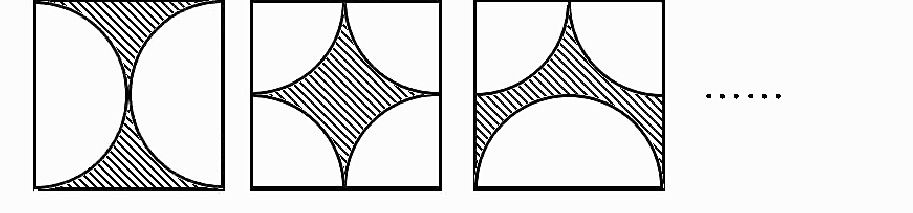
1.观察下图,你有什么发现?
学生发现圆的直径等于正方形的边长,内切圆的面积约为正方形面积的78.5%。

2.不改变图中阴影部分面积的大小,你能对图形进行变化吗?
学生尝试。点明:改变图形的位置,不改变图形的面积,应用“等积变形”思想。
(二)逻辑推理
1.合情推理
如果我们在正方形内画4个圆、9个圆……这些圆的面积之和与外切正方形的面积之间有什么关系?
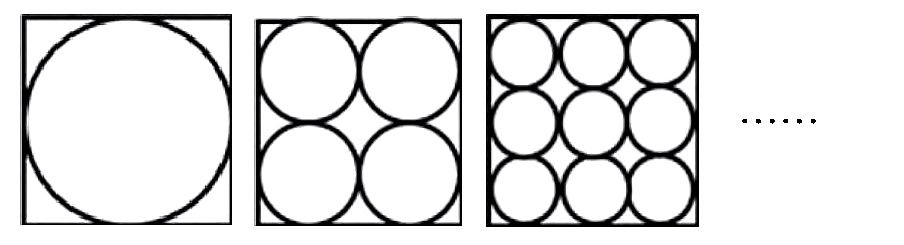
2.尝试验证
(1)举例验证
学生自定小圆的数据,算出每种图形中小圆的面积之和,发现大小是一样的。
(2)逻辑推理
把每个图形分割成对应的正方形,只有1个圆时,圆的面积是:大正方形的面积×78.5%;
有4个圆时,圆的面积之和是:小正方形的面积×78.5%×4=小正方形的面积×4×78.5%=大正方形的面积×78.5%;
有9个圆时,圆的面积之和是:小正方形的面积×78.5%×9=小正方形的面积×9×78.5%=大正方形的面积×78.5%。
(小正方形即每个圆所对应的外切正方形)以此类推,得出每种图形中圆的面积之和的大小是一样的。
(3)总结规律
具有上述排列规律的图形,内切圆的面积之和都约为正方形面积的78.5%。
(三)变化创造
根据上述规律,在不改变图形面积的情况下,试着对图形进行变化创造。
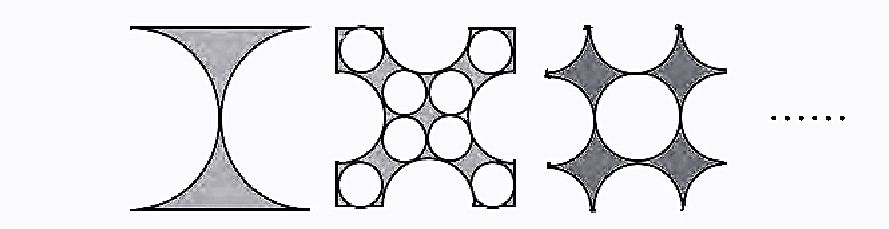
(四)总结提升
回顾这节课的研究过程,发现从简单的情况开始思考,能解决复杂的图形问题。点明:这是一种重要的研究方法。
以正方形内切圆为例,由易及难类推、迁移到多种变式图形,在合情推理与演绎推理的交替中发现变中所蕴含的不变的规律,并由此拓延出多样的创意设计。
这样的专题活动,给予学生的不仅仅是知识与技能的获得,还有对方法的领会和对思想的感悟,更有对数学世界神奇变化的喜爱。
顶一下
(1)
100%
踩一下
(0)
0%
- 发表评论
-
- 最新评论 进入详细评论页>>