“长方体正方体的认识”三种教学设计
一、梳理基础知识
1.交流预习成果
2.比较长方体和正方体异同点
3.长方体和正方体关系
韦恩图
4.引导学生提出问题。
师:对于长方体和正方体,你们还有什么问题?
生:长方体的6个面都是长方形吗?会不会有正方形?
师:好的,这个问题待会儿我们来研究。
二、深化已有认识
● 教学设计(1)
给每个小组提供三种长度的小棒共24根以及16个顶点接口,合作拼搭长方体(框架)。

每个小组只要拼搭出一个长方体,就会发现剩下12根正好拼搭成另一个长方体。
比如,选择一:若三种小棒各选4根,则剩下4根7cm和8根5cm的小棒正好拼搭成两个面是正方形的长方体。通过交流,连步完成填表:
●教学设计(2)
下面有六个长方形(单位1cm)):
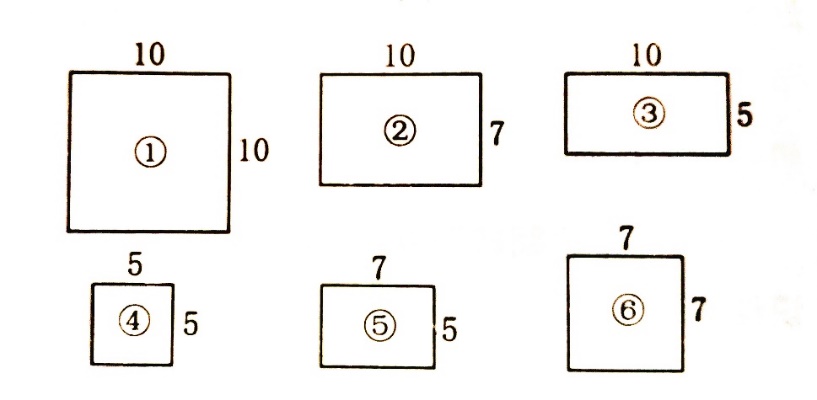
请根据长宽高的变化,选择合适的长方形作长方体的面。
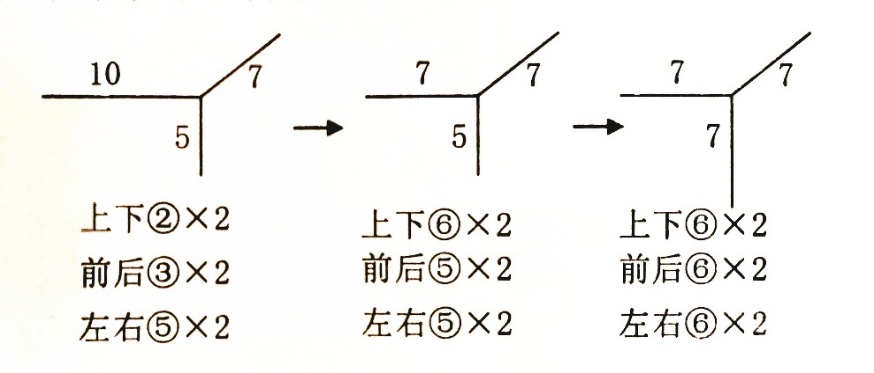
以上两例都是选择棱或面组成长方体。
设计的共同点是数形结合,且着眼于棱与面的尺寸变化,以求发展学生的空间观念,促进学生掌握棱与面的关系。
●教学设计(3)
能否着眼更纯粹的形体认识,获得类似的、更突出的教学效果呢?卞志文、顾文两位老师别开生面的问题设计给我们呈现了一种独特的教学探索与突破,为长方体认识的教学促进学生空间想象提供了新的选择。
(1)问题一(观察、思考)
师:长方体有12个面,那么长方体最多能看到几个面?
生:1个面。(教师在实物投影仪展示1个面的投影)

生:2个面。(教师在实物投影仪展示2个面的投影)

生:3个面。(教师在实物投影仪展示3个面的投影)

师:从正面看、侧面看、上面看只能看到1个面,从1条棱看最多能看到2个面,从1个顶点看最多能看到3个面。为什么最多只能看到3个面?
生:因为看到前面,就看不到后面。
生:看到左面,就看不到右面;看到上面就无法看到下面。
师:是的,相对的两个面只能看到其中一个。
(2)问题二(观察、思考)
师:长方体最多能看到几条棱?
生:最多能看到9条棱。
师:为什么?
生:后面的3条棱隐藏起来,用总棱数减去看不见的棱数,12―3=9条。
(3)问题三(观察、思考)
师:长方体最多能看到几个顶点?
生:有1个顶点无法看到,8―1=7个。
(4)画出“躲起来”的棱与顶点(操作)
师:如果要画出隐藏的面、棱、顶点,怎么画?
学生操作,教师巡视并对独立操作有困难的学生给予指导(利用平移的方法补全棱,交点就是看不到的那个顶点)。
师:大家利用平移的方法补全了看不到的三条棱,隐藏的顶点和“躲起来”的面也都可以“看”到了。
(学生通过数一数、想一想、画一画,解决教师提出的问题,训练画长方体的能力,特别是通过虚线画出看不见的棱。)
(5)问题四(想像)
师:长方体的6个面中可能有几个面是正方形呢?
生:1、3、5个都是不可能的,因为相对的面完全相同。
生:可能有2个面是正方形(教师出示有2个面是正方形的长方体教具)
生:如果6个面都是正方形,就是正方体。
师:有没有可能是4个面呢?(教师出示正方体教具)
生:如果4个面都是正方形,那就是正方体了,也就是6个面都是正方形。
师:长方体只可能有2个面或6个面是正方形。
评析:
①长方体最多能看到几个面、几条棱、几个顶点?
学生的观察顺序正好对应了面、棱、顶点概念的生成顺序:面相交得到棱、棱相交得到顶点。
②怎样画出“躲起来”的面、棱、顶点?
学生通过探索与操作,发现只要补全3条棱,藏在背面的3个面和1个顶点就都出来了,从而通过棱、沟通面与顶点。
③长方体可能有几个面是正方形?
学生能够展开想象与说理,得出只有两种情况的结论。
这些问题都指向长方体基础知识的进一步理解,有效地诱导学生观察、画图想象与思考,在促进空间想象、深化形体认知、培养画图能力的同时,很自然地引发学生依据长方体面、棱的特点进行说理,几何形体的概念思维与空间想象融为了一体。
顶一下
(0)
0%
踩一下
(0)
0%
上一篇:“长方体的认识”教学实践与思考
下一篇:没有了
- 发表评论
-
- 最新评论 进入详细评论页>>